7 Divided By 9 As A Fraction
News Co
Apr 02, 2025 · 5 min read
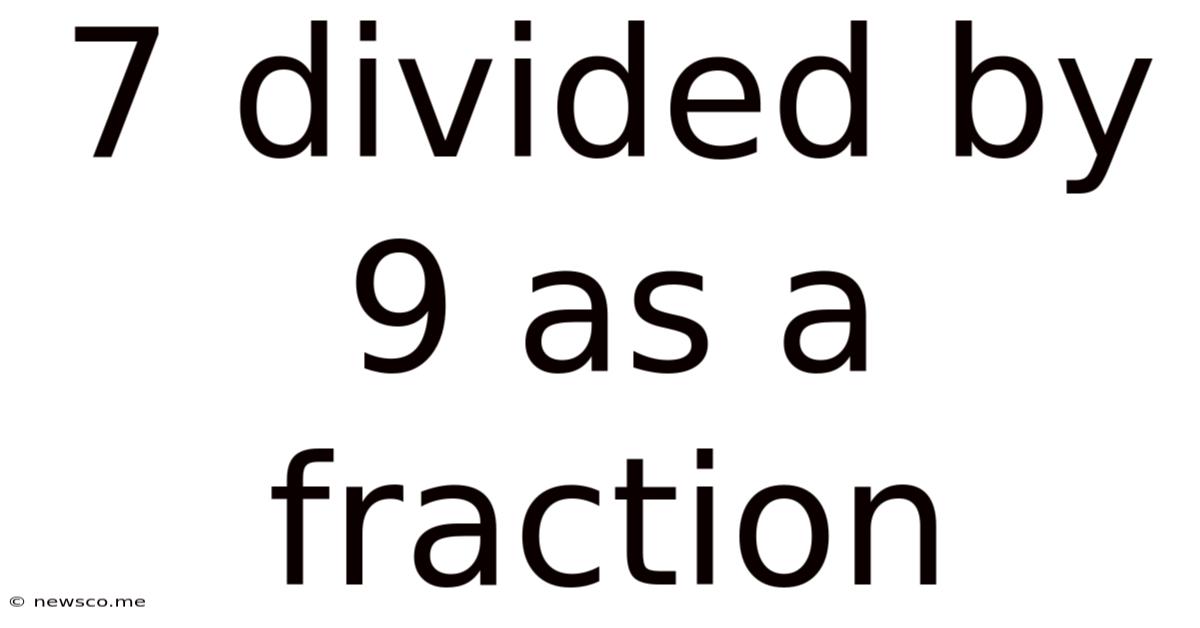
Table of Contents
7 Divided by 9 as a Fraction: A Comprehensive Guide
Dividing 7 by 9 might seem like a simple arithmetic problem, but understanding it thoroughly opens doors to a deeper appreciation of fractions, decimals, and their interconnectedness. This comprehensive guide will explore 7 divided by 9 as a fraction, delving into various representations and applications. We'll unpack the concept, explore its practical uses, and even touch upon related mathematical concepts.
Understanding the Basics: Fractions and Division
Before diving into the specifics of 7 divided by 9, let's refresh our understanding of fractions and their relationship to division. A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
Division, on the other hand, is the process of splitting a quantity into equal parts. When you divide 7 by 9, you're essentially asking, "If I have 7 units and I want to divide them into 9 equal parts, how much will each part be?"
7 Divided by 9: The Fractional Representation
To express 7 divided by 9 as a fraction, we simply write it as:
7/9
The numerator is 7 (the number being divided), and the denominator is 9 (the number we're dividing by). This fraction is already in its simplest form because 7 and 9 share no common factors other than 1. This means it cannot be simplified further.
Decimal Equivalent and its Significance
While 7/9 is a perfectly valid and often preferred representation, it's also useful to understand its decimal equivalent. To find this, we perform the division:
7 ÷ 9 = 0.77777...
Notice the repeating decimal pattern. The '7' continues infinitely. This is denoted mathematically as 0.7̅, with a bar over the 7 to indicate the repeating nature. This decimal representation highlights the fact that 7/9 is a rational number—a number that can be expressed as a fraction of two integers.
The decimal equivalent is particularly useful in practical applications where dealing with fractions might be less intuitive. For example, imagine you're sharing 7 pizzas among 9 people. Instead of saying each person gets 7/9 of a pizza, you could say each person gets approximately 0.777 of a pizza.
Visualizing 7/9: A Pictorial Representation
Understanding fractions can be easier with visual aids. Imagine a circle divided into 9 equal slices. Shading 7 of those slices visually represents the fraction 7/9. This pictorial representation reinforces the concept that 7/9 is less than a whole (a whole circle would be represented by 9/9).
Practical Applications of 7/9
The seemingly simple fraction 7/9 appears in various real-world scenarios:
- Sharing Resources: Dividing resources equally among a group (e.g., pizzas, candy, or work tasks).
- Measurements: Representing portions of a unit of measurement (e.g., 7/9 of a meter, 7/9 of a liter).
- Probability: Calculating probabilities in situations where there are 9 equally likely outcomes, and 7 of them represent a particular event.
- Recipes: Scaling down or up recipes – for instance, using 7/9 of the original amount of an ingredient.
Expanding the Understanding: Related Mathematical Concepts
Understanding 7/9 as a fraction provides a foundation for exploring several related mathematical concepts:
1. Equivalent Fractions:
While 7/9 is in its simplest form, it has numerous equivalent fractions. To find these, multiply both the numerator and denominator by the same non-zero integer. For example:
- 14/18 (multiply by 2)
- 21/27 (multiply by 3)
- 28/36 (multiply by 4)
All these fractions represent the same value as 7/9.
2. Improper Fractions and Mixed Numbers:
An improper fraction is one where the numerator is greater than or equal to the denominator. 7/9 is a proper fraction because the numerator (7) is less than the denominator (9). If we had, for example, 16/9, this would be an improper fraction. Improper fractions can be converted to mixed numbers, which consist of a whole number and a proper fraction. 16/9, for example, is equal to 1 and 7/9.
3. Operations with Fractions:
7/9 can be used in various arithmetic operations:
- Addition: Adding 7/9 to another fraction requires finding a common denominator.
- Subtraction: Similar to addition, subtraction necessitates finding a common denominator.
- Multiplication: Multiplying 7/9 by another fraction involves multiplying the numerators and denominators separately.
- Division: Dividing 7/9 by another fraction involves inverting the second fraction and then multiplying.
4. Percentage Representation:
To express 7/9 as a percentage, we convert the fraction to a decimal (0.7̅) and then multiply by 100:
0.7̅ * 100 ≈ 77.78%
Beyond the Basics: Advanced Concepts
For those seeking a deeper dive, let's explore some more advanced concepts related to 7/9:
1. Continued Fractions:
Any rational number can be expressed as a continued fraction. 7/9 can be represented as a continued fraction, though the process is slightly involved. This representation offers a unique way to express the fraction and might be helpful in advanced mathematical contexts.
2. Applications in Calculus:
While seemingly simple, fractions like 7/9 can appear in calculus when dealing with limits, derivatives, and integrals. The concept of a limit, for example, involves approaching a value (like 7/9) without necessarily reaching it.
3. Number Theory:
In number theory, the study of integers and their properties, concepts like greatest common divisor (GCD) and least common multiple (LCM) become important. Determining the GCD of the numerator and denominator (7 and 9 in this case) helps to simplify fractions.
Conclusion: The Importance of Understanding 7/9
While seemingly a trivial problem, the exploration of 7 divided by 9 as a fraction illuminates fundamental concepts in mathematics. From basic fractional understanding to more advanced concepts like continued fractions and their applications in various fields, the journey through this simple division problem reveals the interconnectedness and depth within mathematics. The ability to confidently work with fractions, decimals, and their interplay is a crucial skill for various academic and real-world applications. This exploration underscores the importance of building a solid foundation in mathematics and the beauty of understanding the seemingly simple. Mastering these fundamental concepts paves the way for tackling more complex mathematical challenges in the future.
Latest Posts
Related Post
Thank you for visiting our website which covers about 7 Divided By 9 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.