7 Pi Over 6 In Degrees
News Co
May 04, 2025 · 5 min read
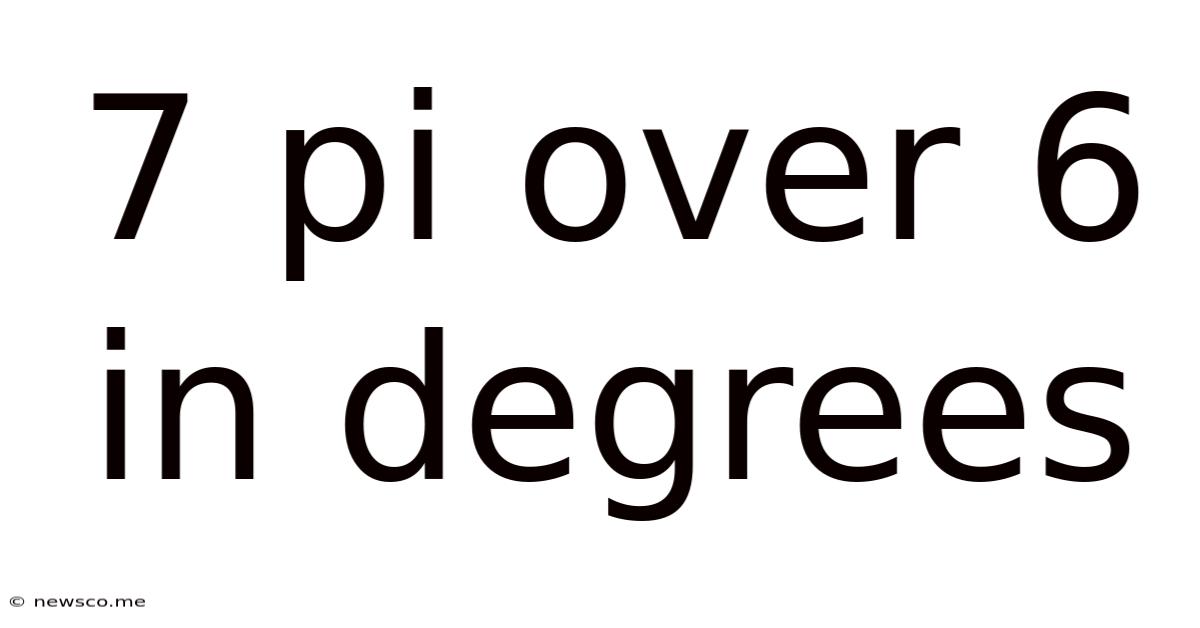
Table of Contents
7π/6 in Degrees: A Comprehensive Exploration of Angles and Radians
Understanding angles and their representation is fundamental in mathematics, particularly in trigonometry and calculus. This article delves deep into the conversion of radians to degrees, focusing specifically on the angle 7π/6 radians. We'll explore its position on the unit circle, its trigonometric values, and its applications in various mathematical contexts. We'll also touch upon practical applications and common pitfalls to avoid.
Understanding Radians and Degrees
Before we tackle 7π/6, let's refresh our understanding of radians and degrees. Both are units used to measure angles, but they differ in their definitions:
-
Degrees: A degree is a unit of measurement of a plane angle, defined as 1/360 of a full rotation. A full circle contains 360 degrees (360°). This system is historically significant and widely used in everyday applications.
-
Radians: A radian is a unit of measurement of a plane angle, defined as the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle. One full rotation in radians is equivalent to 2π radians. Radians are preferred in many mathematical contexts because they simplify calculations and formulas.
The relationship between radians and degrees is crucial for conversion:
2π radians = 360°
This equation provides the basis for converting between the two systems. To convert from radians to degrees, we multiply the radian measure by 180°/π. To convert from degrees to radians, we multiply the degree measure by π/180°.
Converting 7π/6 Radians to Degrees
Now, let's apply this knowledge to our specific angle: 7π/6 radians. Using the conversion factor, we get:
(7π/6 radians) * (180°/π) = (7 * 180°) / 6 = 7 * 30° = 210°
Therefore, 7π/6 radians is equal to 210 degrees.
Locating 7π/6 on the Unit Circle
The unit circle is a powerful tool for visualizing angles and their trigonometric values. The unit circle is a circle with a radius of 1 centered at the origin (0,0) of a Cartesian coordinate system. Angles are measured counterclockwise from the positive x-axis.
To locate 7π/6 on the unit circle:
- Start at the positive x-axis (0° or 0 radians).
- Move counterclockwise. Since 7π/6 is greater than π (180°), it lies in the third quadrant.
- Divide the circle: Imagine dividing the circle into six equal parts. Each part represents π/3 radians or 60°. 7π/6 is one part past the 180° mark, putting it at 210°.
The coordinates of the point on the unit circle corresponding to 7π/6 are (-√3/2, -1/2).
Trigonometric Values of 7π/6
The coordinates on the unit circle directly relate to the trigonometric functions of the angle:
- sin(7π/6) = -1/2 (The y-coordinate)
- cos(7π/6) = -√3/2 (The x-coordinate)
- tan(7π/6) = sin(7π/6) / cos(7π/6) = (-1/2) / (-√3/2) = 1/√3 = √3/3
These values are crucial for solving trigonometric equations and problems involving triangles.
Applications of 7π/6 in Various Mathematical Contexts
The angle 7π/6, or its equivalent 210°, finds applications in numerous mathematical areas:
1. Trigonometry:
Solving triangles, particularly those involving oblique triangles (triangles without a right angle), often requires understanding angles beyond the first quadrant. The trigonometric functions of 7π/6 are essential in such calculations using the Law of Sines and the Law of Cosines.
2. Calculus:
In calculus, understanding angles in radians is critical. Derivatives and integrals of trigonometric functions are most easily calculated when using radians. Furthermore, the concept of radians is fundamental in understanding concepts like arc length and sector area calculations.
3. Physics and Engineering:
Many physics and engineering applications involve oscillatory motion (like simple harmonic motion) or rotational motion. These problems frequently utilize trigonometric functions to describe the position, velocity, and acceleration of objects, often making use of angles expressed in radians.
4. Computer Graphics and Game Development:
In computer graphics and game development, the representation and manipulation of angles are essential for rendering scenes, calculating object positions, and managing rotations. Understanding radians and degrees is crucial for accurate calculations and realistic visual representations.
Common Pitfalls and How to Avoid Them
While converting radians to degrees might seem straightforward, here are a few common mistakes to watch out for:
- Incorrect use of the conversion factor: Make sure to use the correct conversion factor (180°/π or π/180°) depending on whether you are converting from radians to degrees or vice versa.
- Incorrect placement on the unit circle: Carefully consider the quadrant and the sign of the trigonometric values. The quadrant determines the sign of the sine, cosine, and tangent.
- Calculator settings: Ensure that your calculator is set to the correct angle mode (radians or degrees) when performing calculations. Otherwise, you may get incorrect results.
- Forgetting the negative signs: Remember that the sine and cosine values can be negative in certain quadrants (II, III, and IV).
Advanced Concepts and Further Exploration
For those seeking a more advanced understanding, exploring these concepts would provide a deeper appreciation of 7π/6 radians and its role in mathematics:
- Complex numbers: Angles in radians play a crucial role in the representation of complex numbers in polar form.
- Series expansions of trigonometric functions: Understanding the Taylor or Maclaurin series expansions of trigonometric functions often involves radians.
- Differential equations: Many differential equations, particularly those involving oscillations, utilize trigonometric functions and their relationships with angles in radians.
Conclusion
The seemingly simple angle 7π/6 radians, equivalent to 210°, serves as a foundational element in understanding the broader world of angles, trigonometry, and their applications across diverse fields. By mastering the conversion between radians and degrees, understanding its position on the unit circle, and appreciating its trigonometric values, you lay a solid groundwork for tackling more advanced mathematical concepts and real-world applications. Remember to practice consistently and avoid the common pitfalls highlighted to ensure accuracy in your calculations. The journey of understanding 7π/6, and angles in general, is a continuous process of learning and exploration.
Latest Posts
Latest Posts
-
How To Find Average Speed With Two Speeds
May 05, 2025
-
What Triangle Has Two Equal Sides
May 05, 2025
-
How Many Millimeters In 5 Liters
May 05, 2025
-
Half Of 1 3 4 Cup Of Flour
May 05, 2025
-
Whats 25 Percent Off Of 60
May 05, 2025
Related Post
Thank you for visiting our website which covers about 7 Pi Over 6 In Degrees . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.