75 Out Of 90 As A Percentage
News Co
Mar 27, 2025 · 5 min read
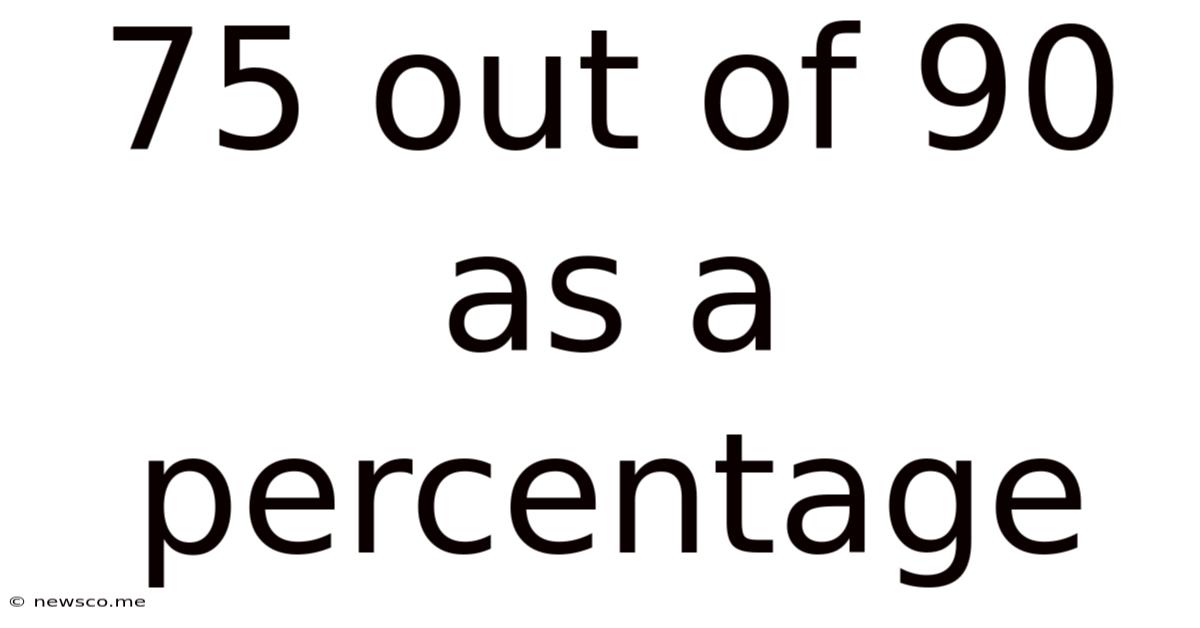
Table of Contents
75 out of 90 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from academic assessments to financial transactions. Understanding how to convert fractions to percentages is crucial for interpreting data, making informed decisions, and communicating numerical information effectively. This article delves deep into the calculation of 75 out of 90 as a percentage, exploring multiple methods, real-world applications, and offering insights into percentage calculations in general.
Understanding Percentages
Before diving into the specific calculation, let's solidify the foundational concept of percentages. A percentage represents a fraction of 100. The term "percent" literally means "out of 100" ("per cent"). Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Calculating 75 out of 90 as a Percentage: Method 1 – The Fraction Method
The most straightforward method involves converting the given numbers into a fraction and then converting that fraction into a percentage.
-
Form a Fraction: Represent "75 out of 90" as a fraction: 75/90.
-
Simplify the Fraction (Optional but Recommended): Simplifying the fraction makes the conversion to a percentage easier. Both 75 and 90 are divisible by 15. Simplifying, we get: 75/90 = 5/6.
-
Convert to a Decimal: Divide the numerator (5) by the denominator (6): 5 ÷ 6 ≈ 0.8333.
-
Convert to a Percentage: Multiply the decimal by 100: 0.8333 × 100 = 83.33%.
Therefore, 75 out of 90 is 83.33%.
Calculating 75 out of 90 as a Percentage: Method 2 – The Proportion Method
This method utilizes the concept of proportions to solve for the percentage.
-
Set up a Proportion: We can set up a proportion to solve this problem:
75/90 = x/100
Where 'x' represents the percentage we're trying to find.
-
Cross-Multiply: Cross-multiply the terms:
90x = 7500
-
Solve for x: Divide both sides by 90:
x = 7500/90 = 83.33
-
Express as a Percentage: Therefore, x = 83.33%, confirming our previous result.
Calculating 75 out of 90 as a Percentage: Method 3 - Using a Calculator
Most calculators have a percentage function. Simply enter 75 ÷ 90 and then multiply the result by 100. The calculator will directly provide the answer: 83.33%. This is the quickest method, especially when dealing with more complex calculations.
Real-World Applications of Percentage Calculations
The ability to calculate percentages efficiently has practical implications across a wide spectrum of real-life scenarios:
1. Academic Performance:
- Grade Calculations: Many educational systems use percentages to represent student performance on tests, assignments, and overall course grades. Understanding percentage calculations helps students track their progress and identify areas needing improvement. For example, if a student scores 75 out of 90 on an exam, they can easily calculate their percentage score (83.33%) to understand their performance relative to the total possible points.
2. Financial Matters:
-
Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Calculating interest earned or paid is crucial for managing personal finances effectively.
-
Discounts and Sales: Stores regularly offer discounts expressed as percentages. Being able to quickly calculate the discounted price is essential for making informed purchasing decisions. For instance, a 20% discount on an item priced at $100 would reduce the price by $20 ($100 x 0.20), resulting in a final price of $80.
-
Taxes: Taxes are frequently levied as a percentage of income or the value of goods and services. Understanding tax calculations is critical for financial planning and compliance.
-
Investment Returns: Investors use percentages to track the performance of their investments. Calculating the percentage return on investment is vital for evaluating the success of different investment strategies.
3. Data Analysis and Statistics:
-
Surveys and Polls: Percentages are widely used to represent the results of surveys and polls. Researchers use percentages to summarize the responses and draw meaningful conclusions from the data.
-
Data Visualization: Charts and graphs often use percentages to display data visually. Understanding percentages facilitates the interpretation of such visual representations.
4. Everyday Life:
-
Tipping: Many people calculate tips as a percentage of the total bill in restaurants or other service-oriented establishments.
-
Recipe Scaling: When cooking, adjusting recipes based on the number of servings often involves percentage calculations. For example, if a recipe calls for 1 cup of flour and you want to double the recipe, you'll need to increase the flour by 100% (1 cup x 2 = 2 cups).
Beyond the Basics: Advanced Percentage Calculations
While calculating 75 out of 90 is a relatively straightforward example, the principles extend to more complex scenarios. For instance:
-
Calculating Percentage Increase or Decrease: Determining the percentage change between two values involves finding the difference between the two values, dividing by the original value, and then multiplying by 100.
-
Finding the Original Value: If you know the percentage and the final value, you can work backward to find the original value using algebraic equations.
-
Compounding Percentages: In situations involving compound interest or repeated percentage changes, the calculations become more intricate, often requiring exponential formulas.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The more you practice percentage calculations, the more comfortable and efficient you'll become.
-
Use Different Methods: Experiment with various methods (fraction, proportion, calculator) to find the approach that best suits your understanding and the specific problem.
-
Understand the Context: Always consider the context of the problem to ensure your calculations are relevant and meaningful.
-
Check Your Work: Always double-check your calculations to avoid errors.
Conclusion
Calculating 75 out of 90 as a percentage, resulting in 83.33%, is a simple yet fundamental application of percentage calculations. Understanding percentages is a crucial skill applicable to numerous aspects of life, from academics and finances to data analysis and everyday decisions. Mastering percentage calculations empowers you to interpret data effectively, make informed choices, and navigate the quantitative aspects of the world around you with confidence. By employing the methods outlined in this article and practicing regularly, you can build a strong foundation in percentage calculations and enhance your problem-solving capabilities significantly.
Latest Posts
Related Post
Thank you for visiting our website which covers about 75 Out Of 90 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.