8 Of What Number Is 2
News Co
May 08, 2025 · 5 min read
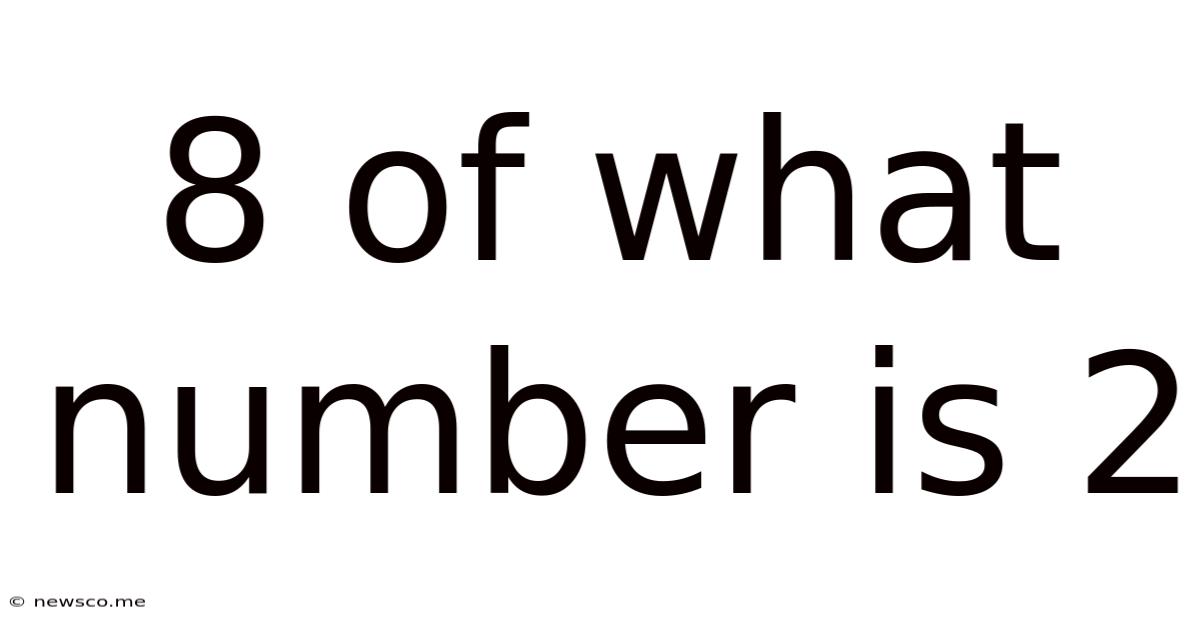
Table of Contents
8 of What Number is 2? Unveiling the Power of Proportion and Algebra
This seemingly simple question, "8 of what number is 2?", opens a door to a fascinating world of mathematical concepts, problem-solving techniques, and real-world applications. While the immediate answer might seem elusive, understanding the underlying principles reveals its straightforward solution and highlights the broader significance of proportional reasoning and algebraic thinking. This article will delve into various methods for solving this problem, exploring its connection to percentages, ratios, and equations, ultimately demonstrating how seemingly basic mathematical inquiries can pave the way for more complex problem-solving scenarios.
Understanding the Problem: Deconstructing "8 of What Number is 2?"
The core of the question lies in understanding the relationship between parts and wholes. It asks: "If 8 represents a certain fraction of an unknown whole number, and that fraction equals 2, what is the value of the whole number?" This phrasing subtly introduces the concept of proportion – a fundamental concept in mathematics and science where two ratios are equivalent.
Identifying Key Elements:
- The Part: This is the known value, which is 2.
- The Whole: This is the unknown value, which we need to find. Let's represent it with the variable 'x'.
- The Fraction or Ratio: This represents the relationship between the part and the whole. In this case, it's 8/x.
Method 1: Solving with Proportions
Proportions offer a visually intuitive and effective way to solve this problem. We can set up the proportion as follows:
8/x = 2/1
This equation states that the ratio of 8 to the unknown number (x) is equal to the ratio of 2 to 1 (which is simply 2). To solve for x, we can cross-multiply:
8 * 1 = 2 * x
This simplifies to:
8 = 2x
Now, we can solve for x by dividing both sides of the equation by 2:
x = 8/2
x = 4
Therefore, 8 of 4 is 2.
Method 2: Solving with Algebra
This approach utilizes algebraic equations to represent the problem. We can translate the statement "8 of what number is 2" into an algebraic equation:
(8/100) * x = 2
This equation represents 8 percent (8 out of 100) of an unknown number (x) being equal to 2. To solve for x:
x = 2 / (8/100)
x = 2 * (100/8)
x = 200/8
x = 25
This shows that 8% of 25 is 2. Note that here we assume the "of" implies a percentage relationship. The initial problem statement is ambiguous; however, if "of" implies multiplication, we use the first approach.
Method 3: Using Reverse Percentage
The phrase "8 of what number is 2" can be interpreted as finding the number which has a percentage of 8% equal to 2. To do this, we can use the reverse percentage calculation:
- Identify the percentage: 8%
- Identify the resulting value: 2
- Calculate the whole number: (2 / 8) * 100 = 25
This confirms that 8% of 25 is 2.
Choosing the Right Method
The choice of method depends on the context and the preferred approach. For this particular problem, the proportional method (Method 1) is the most direct and intuitive approach if the “of” implies multiplication, while Method 2 (algebra) offers a more generalized method suited for more complex scenarios. Method 3 is more suited when interpreting "of" as pertaining to percentages. The key is understanding the underlying relationship between the parts and the whole.
Real-World Applications: Proportion and Percentage in Everyday Life
Understanding proportions and percentages is crucial in many everyday situations. Consider these examples:
-
Cooking: Scaling recipes up or down requires understanding proportions. If a recipe calls for 2 cups of flour and makes 8 servings, how much flour is needed for 16 servings? This involves setting up a proportion and solving for the unknown quantity of flour.
-
Shopping: Discounts are often expressed as percentages. If a store offers a 20% discount on an item that originally costs $50, calculating the final price requires understanding percentage calculations.
-
Finance: Interest rates, loan payments, and investments all involve percentage calculations. Understanding these concepts is vital for making informed financial decisions.
-
Science: Many scientific experiments involve measuring proportions and percentages. Analyzing experimental data often involves comparing ratios and understanding the relationships between variables.
-
Data Analysis: Percentages and proportions are essential tools in interpreting data and visualizing relationships between different variables in charts, graphs, and other data representations. Interpreting data correctly is crucial for effective decision-making in many sectors.
Expanding the Concept: Beyond Simple Proportions
While the problem "8 of what number is 2" seems simple, it lays a strong foundation for more complex problems involving ratios, proportions, percentages, and algebraic equations. These concepts are building blocks for understanding more advanced mathematical topics, including:
- Linear Equations: Solving equations with multiple variables requires understanding proportional relationships.
- Geometry: Similar triangles and other geometric figures involve understanding ratios and proportions.
- Calculus: Derivatives and integrals often involve calculating rates of change, which are essentially proportional relationships.
- Statistics: Understanding proportions and percentages is fundamental to analyzing data and interpreting probabilities.
Conclusion: The Power of Simple Problems
The question, "8 of what number is 2?" may seem trivial at first glance. However, by exploring different methods of solving it, we've uncovered the underlying principles of proportional reasoning and algebraic thinking. This seemingly basic problem highlights the importance of understanding fundamental mathematical concepts and their wide-ranging applications in daily life and more advanced mathematical fields. Mastering these principles opens doors to tackling more complex problems and fostering a deeper appreciation for the power of mathematics in understanding and interpreting the world around us. From everyday tasks to scientific endeavors, the ability to confidently work with proportions and percentages is an invaluable skill. Therefore, understanding the solution to this problem – and the methods employed to arrive at it – provides a significant step forward in developing a strong mathematical foundation.
Latest Posts
Related Post
Thank you for visiting our website which covers about 8 Of What Number Is 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.