80 Is 20 Of What Number
News Co
Apr 17, 2025 · 5 min read
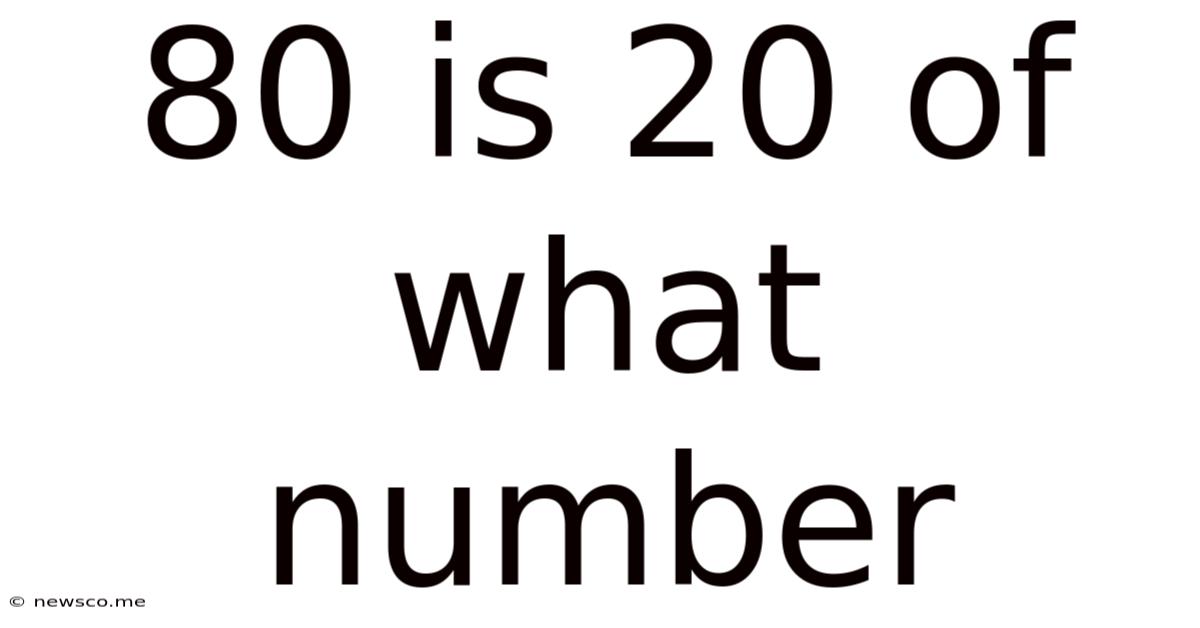
Table of Contents
80 is 20% of What Number? A Comprehensive Guide to Percentage Calculations
Solving percentage problems is a fundamental skill with applications across various fields, from everyday budgeting to complex scientific calculations. Understanding how to determine the whole from a percentage and its part is particularly crucial. This article will delve into the intricacies of solving the problem "80 is 20% of what number?", providing multiple approaches and demonstrating the underlying principles. We'll also explore practical applications and extend the concept to handle more complex percentage scenarios.
Understanding the Basics of Percentages
Before tackling the specific problem, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 20% can be written as the fraction 20/100 or the decimal 0.20.
Key Terms and Concepts
- Percentage: A portion or fraction of a whole, expressed as a number out of 100.
- Part: The specific amount representing the percentage of the whole. (In our problem, this is 80)
- Whole: The total amount from which the percentage is taken. (This is what we need to find.)
- Rate: The percentage itself, expressed as a decimal or fraction. (In our problem, this is 20% or 0.20)
Method 1: Using the Formula
The most straightforward method to solve "80 is 20% of what number?" involves using a standard percentage formula:
Part = Rate × Whole
In our problem:
- Part = 80
- Rate = 20% = 0.20
- Whole = x (this is what we need to find)
Substituting these values into the formula, we get:
80 = 0.20 × x
To solve for x, we divide both sides of the equation by 0.20:
x = 80 / 0.20
x = 400
Therefore, 80 is 20% of 400.
Method 2: Using Proportions
Another effective approach involves setting up a proportion. A proportion is a statement that two ratios are equal. We can set up a proportion based on the given information:
80/x = 20/100
This proportion states that the ratio of the part (80) to the whole (x) is equal to the ratio of the percentage (20) to 100. To solve for x, we can cross-multiply:
80 × 100 = 20 × x
8000 = 20x
x = 8000 / 20
x = 400
Again, we arrive at the solution: 80 is 20% of 400.
Method 3: Using the Decimal Equivalent
As mentioned earlier, a percentage can be easily converted to its decimal equivalent. We can directly use this decimal equivalent in our calculation:
20% = 0.20
We know that 80 represents 20% of the unknown number. So, we can set up the equation:
0.20 * x = 80
Solving for x:
x = 80 / 0.20
x = 400
This method reiterates the solution: 80 is 20% of 400.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world scenarios:
1. Finance and Budgeting:
- Calculating discounts: If an item is discounted by 20%, determining the original price from the discounted price requires using percentage calculations.
- Analyzing interest rates: Understanding the relationship between principal, interest rate, and accumulated interest involves percentage calculations.
- Tracking expenses: Determining the percentage of income spent on different categories helps manage finances effectively.
- Investing and returns: Calculating investment returns and understanding growth percentages are vital in investment strategies.
2. Sales and Marketing:
- Conversion rates: Measuring the percentage of website visitors who complete a desired action (e.g., making a purchase) is critical for marketing analysis.
- Market share analysis: Determining the percentage of the market held by a particular company provides valuable insights into market position.
- Sales growth: Tracking percentage increases or decreases in sales over time indicates business performance.
3. Science and Engineering:
- Data analysis: Percentages are frequently used to express proportions and probabilities in scientific research.
- Error analysis: Scientists use percentages to represent the margin of error in experimental data.
- Scaling and proportions: Percentage calculations are crucial in scaling up or down designs and models.
4. Everyday Life:
- Tip calculations: Calculating tips at restaurants involves percentage calculations.
- Sales tax: Understanding how sales tax increases the final price of a product requires percentage calculations.
- Nutrition labels: Interpreting the percentage of daily value for nutrients on food labels relies on percentage understanding.
Extending the Concept: More Complex Percentage Problems
While the problem "80 is 20% of what number?" provides a foundational understanding, percentage problems can become more complex. For instance:
- Finding the percentage increase or decrease: These problems involve calculating the percentage change between two values.
- Calculating multiple percentages: Some scenarios may involve calculating a series of percentages applied sequentially.
- Compound interest calculations: Compound interest problems involve calculating interest on both the principal and accumulated interest.
These more complex problems often require a deeper understanding of algebraic manipulation and sometimes the use of financial calculators or spreadsheets.
Conclusion: Mastering Percentage Calculations
The ability to solve percentage problems, even seemingly simple ones like "80 is 20% of what number?", is a valuable skill applicable across various aspects of life. By understanding the fundamental formulas, employing different solution methods, and exploring practical applications, you'll be well-equipped to confidently tackle a wide range of percentage-related challenges. Remember that mastering this skill involves practice and applying the concepts to diverse real-world scenarios. Consistent practice will strengthen your ability to solve these problems efficiently and accurately. From budgeting to business analysis, the ability to work confidently with percentages will be an invaluable asset.
Latest Posts
Related Post
Thank you for visiting our website which covers about 80 Is 20 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.