80 Is 40 Percent Of What Number
News Co
May 08, 2025 · 4 min read
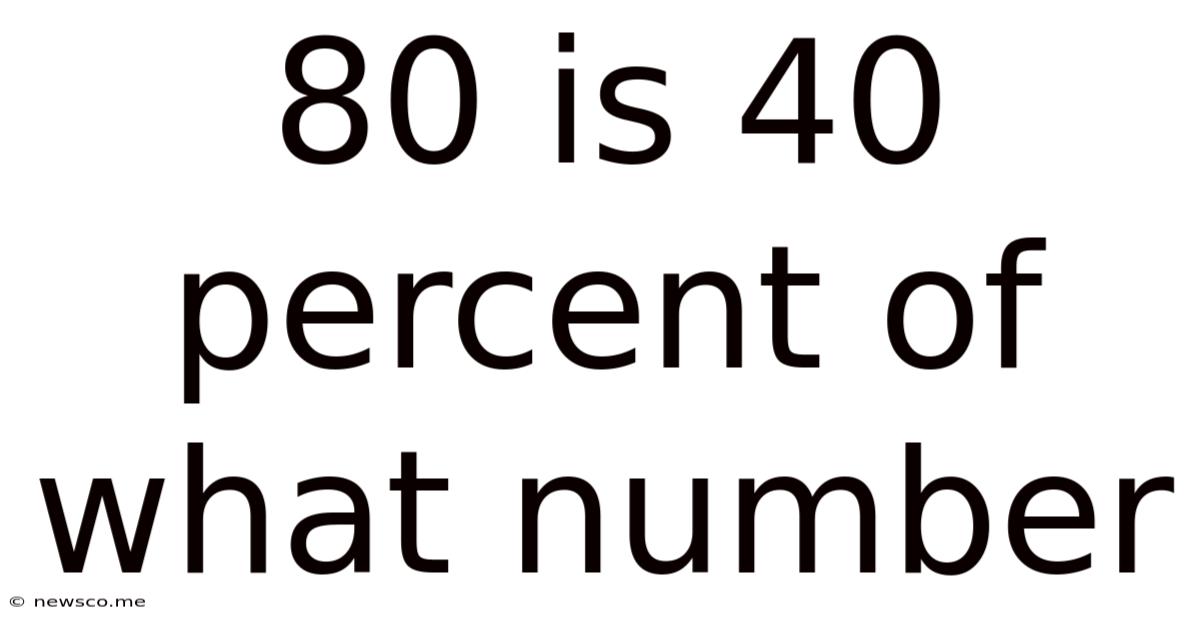
Table of Contents
80 is 40 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article delves deep into the question, "80 is 40 percent of what number?", providing a step-by-step solution, exploring different approaches, and offering practical applications to solidify your understanding of percentage calculations.
Understanding the Problem: 80 is 40% of X
The core of the problem lies in translating the statement "80 is 40 percent of what number?" into a mathematical equation. We can represent this as:
80 = 0.40 * X
Where:
- 80 represents the part (or percentage) we know.
- 0.40 (or 40/100) represents the percentage (40%).
- X represents the unknown whole number we need to find.
Method 1: Algebraic Solution
This method utilizes basic algebra to solve for the unknown variable, X. The steps are as follows:
-
Rewrite the equation: Start with the equation we established: 80 = 0.40 * X
-
Isolate X: To solve for X, we need to isolate it on one side of the equation. We can do this by dividing both sides of the equation by 0.40:
80 / 0.40 = (0.40 * X) / 0.40
-
Simplify: This simplifies to:
X = 200
Therefore, 80 is 40 percent of 200.
Method 2: Using Proportions
Proportions offer another effective way to solve percentage problems. A proportion is simply an equation stating that two ratios are equal. We can set up a proportion as follows:
Part / Whole = Percentage / 100
In our case:
- Part: 80
- Percentage: 40
- Whole: X (what we need to find)
So the proportion becomes:
80 / X = 40 / 100
To solve this proportion:
-
Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa:
80 * 100 = 40 * X
-
Simplify: This gives us:
8000 = 40X
-
Solve for X: Divide both sides by 40:
X = 8000 / 40 = 200
Again, we find that X = 200.
Method 3: The Percentage Formula
A more generalized formula for percentage problems is:
Percentage = (Part / Whole) * 100
We can rearrange this formula to solve for the "Whole" (which is our X in this case):
Whole = (Part / Percentage) * 100
Plugging in our values:
Whole = (80 / 40) * 100 = 2 * 100 = 200
This method confirms our previous results, showing that 80 is 40 percent of 200.
Practical Applications: Real-World Examples
Understanding percentage calculations extends beyond simple mathematical exercises. Here are some practical applications:
1. Sales and Discounts:
Imagine a store is offering a 40% discount on an item. If the discounted price is $80, you can use the methods described above to find the original price. The original price was $200.
2. Financial Calculations:
Percentage calculations are crucial in finance. For example, determining interest earned on savings accounts, calculating loan payments, and analyzing investment returns all involve percentage calculations. Understanding the fundamental principles allows for better financial decision-making.
3. Data Analysis:
In data analysis and statistics, percentages are used to represent proportions and trends within datasets. For instance, if 80 out of 200 survey respondents answered "yes" to a question, this represents a 40% "yes" response rate.
4. Scientific and Engineering Applications:
Percentages are widely used in science and engineering for representing efficiency, error rates, and other relevant quantities. For example, expressing the efficiency of a machine as a percentage of its theoretical maximum capacity.
Expanding Your Understanding: Beyond the Basics
While this article focused on solving "80 is 40 percent of what number?", the underlying principles can be applied to a wide range of percentage problems. Here are some variations to challenge and expand your understanding:
- Finding the percentage: What percentage of 200 is 80? (Answer: 40%)
- Finding the part: What is 40% of 200? (Answer: 80)
- More complex scenarios: Problems involving multiple percentages, consecutive discounts, or compound interest require a deeper understanding of percentage calculations but build upon the same fundamental principles.
Conclusion: Mastering Percentage Calculations
The ability to solve percentage problems, like determining what number 80 represents 40% of, is a highly valuable skill. By understanding the different methods—algebraic solutions, proportions, and the percentage formula—and practicing with real-world examples, you can strengthen your understanding and confidently tackle various percentage-related challenges. This knowledge is applicable across many fields, empowering you to make informed decisions in personal finance, data analysis, and more. Remember that consistent practice is key to mastering this fundamental mathematical concept. Try working through different percentage problems and apply these methods to real-life situations to further solidify your understanding. The more you practice, the easier and more intuitive these calculations will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about 80 Is 40 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.