80 Of 50 Is What Number
News Co
Mar 27, 2025 · 4 min read
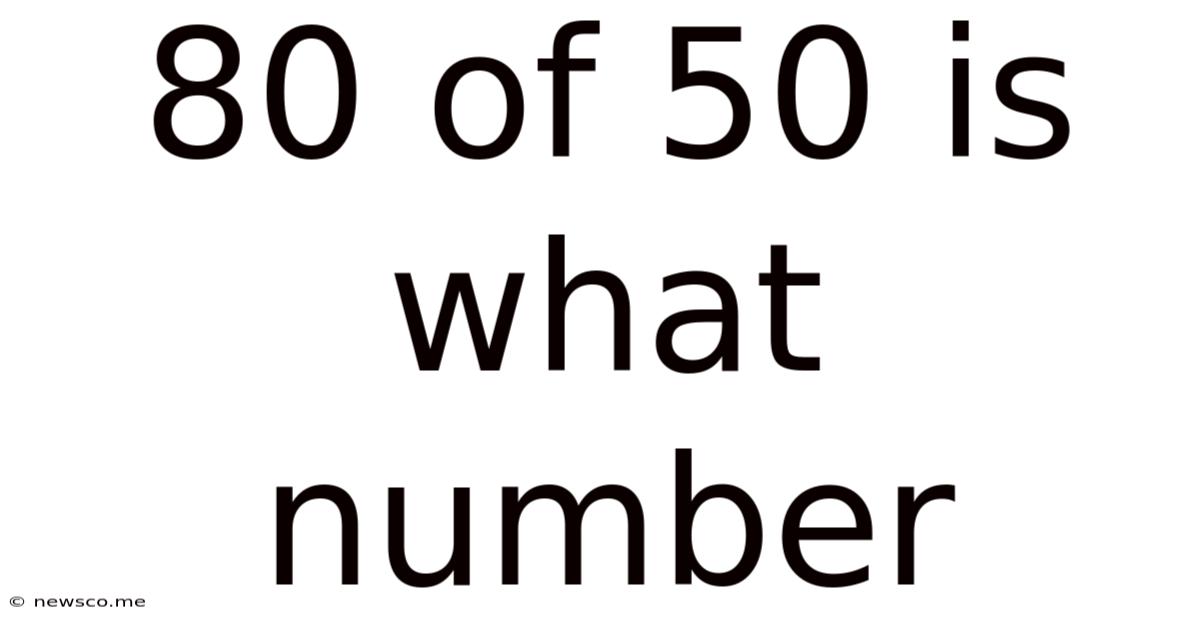
Table of Contents
80% of 50 is What Number: A Comprehensive Guide to Percentages
Calculating percentages is a fundamental skill applicable across various aspects of life, from everyday finances to complex scientific analyses. Understanding how to determine a percentage of a number is crucial for budgeting, understanding discounts, calculating taxes, and much more. This article will delve deep into the calculation of "80% of 50," exploring different methods, providing practical examples, and offering broader insights into percentage calculations.
Understanding Percentages
Before we tackle the specific problem of finding 80% of 50, let's establish a clear understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 25% means 25 out of 100, which can also be written as the fraction 25/100 or the decimal 0.25.
Key Concepts:
- Fraction: A percentage can be easily converted into a fraction by placing the percentage value over 100. For example, 80% = 80/100.
- Decimal: Percentages can also be represented as decimals. To convert a percentage to a decimal, divide the percentage by 100. Thus, 80% = 80 ÷ 100 = 0.80.
- Whole Number: The number of which you are finding the percentage is called the whole number or base. In our case, 50 is the whole number.
Calculating 80% of 50: Three Methods
There are several ways to calculate 80% of 50. Let's examine three common methods:
Method 1: Using the Fraction Method
This method involves converting the percentage into a fraction and then multiplying it by the whole number.
-
Convert the percentage to a fraction: 80% = 80/100. This fraction can be simplified to 4/5 by dividing both the numerator and denominator by 20.
-
Multiply the fraction by the whole number: (4/5) * 50 = 4 * (50/5) = 4 * 10 = 40
Therefore, 80% of 50 is $\boxed{40}$.
Method 2: Using the Decimal Method
This method utilizes the decimal equivalent of the percentage.
-
Convert the percentage to a decimal: 80% = 80 ÷ 100 = 0.80
-
Multiply the decimal by the whole number: 0.80 * 50 = 40
Again, 80% of 50 is $\boxed{40}$.
Method 3: Using Proportions
This method involves setting up a proportion to solve for the unknown value.
-
Set up the proportion: Let 'x' represent 80% of 50. The proportion can be written as:
80/100 = x/50
-
Cross-multiply: 100x = 80 * 50
-
Solve for x: 100x = 4000 => x = 4000/100 => x = 40
This confirms that 80% of 50 is $\boxed{40}$.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages has numerous real-world applications. Here are a few examples:
1. Sales and Discounts:
Imagine a store offering an 80% discount on an item originally priced at $50. Using the methods described above, you can quickly calculate the discount amount ($40) and the final price ($10). This allows you to make informed purchasing decisions.
2. Tax Calculations:
Sales tax is often expressed as a percentage. If the sales tax in your area is 8%, and you buy an item for $50, you can calculate the tax amount using the same percentage calculation methods.
3. Tip Calculation:
When dining out, it's customary to leave a tip, often expressed as a percentage of the bill. If you want to leave an 80% tip (though this is quite generous!), you can calculate the tip amount on a $50 bill using the familiar methods.
4. Grade Calculation:
Percentage calculations are essential in academic settings. If you scored 40 out of 50 on a test, you can calculate your percentage score (80%) to understand your performance.
5. Financial Analysis:
In finance, percentages are crucial for analyzing investment returns, calculating interest rates, understanding profit margins, and assessing financial risk.
Expanding Your Understanding of Percentages
While this article focuses on calculating 80% of 50, the underlying principles extend to all percentage calculations. Mastering these principles empowers you to solve a wide range of percentage problems.
Calculating x% of y: A General Formula
The general formula for calculating x% of y is:
(x/100) * y
Where:
- x represents the percentage.
- y represents the whole number.
This formula works for any percentage and any whole number, making it a versatile tool for diverse applications.
Inverse Percentage Problems: Finding the Whole Number
Sometimes, you know the percentage and the resulting value, but need to find the original whole number. These are called inverse percentage problems. Let's say you know that 80% of a number is 40. To find the original number, you would set up the equation:
0.80 * y = 40
Solving for y:
y = 40 / 0.80 = 50
This demonstrates how to work backward from a percentage and its result to find the original whole number.
Conclusion: Mastering Percentage Calculations
Understanding percentages is a crucial skill with broad applications in everyday life and professional settings. Whether you are calculating discounts, taxes, tips, grades, or analyzing financial data, the ability to confidently work with percentages is invaluable. This article has provided a comprehensive guide to calculating 80% of 50, exploring different methods and highlighting the importance of mastering percentage calculations for various real-world scenarios. Remember to practice these methods to build proficiency and confidence in your ability to handle percentage-based problems. The more you practice, the easier and more intuitive these calculations will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about 80 Of 50 Is What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.