80 Of C Is 20 What Is C
News Co
May 07, 2025 · 5 min read
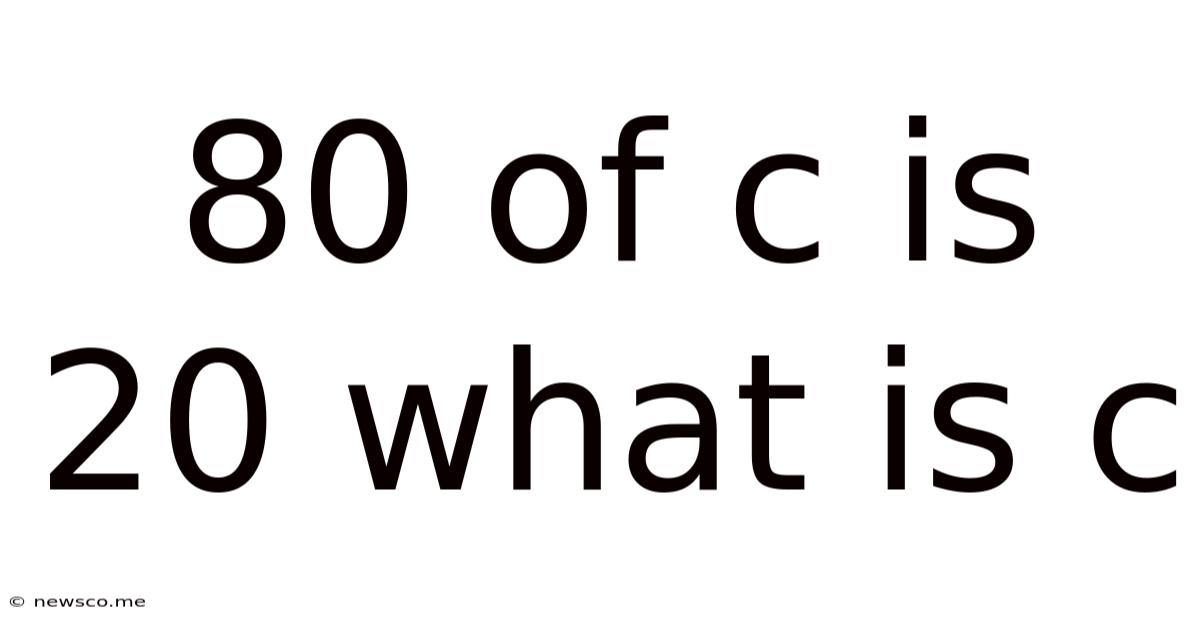
Table of Contents
Solving for "C": A Deep Dive into the Equation "80% of C is 20"
This seemingly simple mathematical equation, "80% of C is 20," presents a valuable opportunity to explore several mathematical concepts and problem-solving techniques. While the answer might seem immediately obvious to some, a deeper dive reveals opportunities to understand percentage calculations, algebraic manipulation, and even the practical applications of this type of problem in various fields. This article will guide you through multiple methods of solving this equation, explaining the reasoning behind each step and offering insights into broader mathematical principles.
Understanding Percentages and the Equation
Before diving into the solution, let's clearly define the problem: We are given the statement "80% of C is 20." This translates directly into a mathematical equation:
0.80 * C = 20
Here:
- 0.80 represents 80% expressed as a decimal (80/100 = 0.80).
- C is the unknown variable we need to solve for.
- 20 is the result of 80% of C.
This equation is a fundamental example of a linear equation, one of the most basic yet widely used equation types in mathematics. Understanding how to solve these equations is crucial for various quantitative reasoning tasks.
Method 1: Direct Algebraic Solution
The most straightforward method to solve for C is through direct algebraic manipulation. Our goal is to isolate C on one side of the equation. We can achieve this by dividing both sides of the equation by 0.80:
0.80 * C / 0.80 = 20 / 0.80
This simplifies to:
C = 25
Therefore, the value of C is 25. This method is efficient and demonstrates a fundamental algebraic principle: performing the same operation on both sides of an equation maintains its equality.
Method 2: Using Proportions
Another approach involves setting up a proportion. We know that 80% of C is 20. We can express this as a ratio:
80/100 = 20/C
This proportion states that the ratio of 80 to 100 is equivalent to the ratio of 20 to C. To solve for C, we can cross-multiply:
80 * C = 20 * 100
80C = 2000
Now, divide both sides by 80:
C = 2000 / 80
C = 25
Again, we arrive at the solution: C = 25. This method highlights the power of proportions in solving percentage-related problems, illustrating the relationship between parts and the whole.
Method 3: Working with Fractions
Instead of using decimals, we can work directly with fractions. The equation "80% of C is 20" can be written as:
(80/100) * C = 20
Simplify the fraction:
(4/5) * C = 20
To isolate C, multiply both sides by the reciprocal of 4/5, which is 5/4:
(5/4) * (4/5) * C = 20 * (5/4)
This simplifies to:
C = 100 / 4
C = 25
This method reinforces the understanding of fractions and their role in percentage calculations, showcasing an alternative approach to solving the equation.
Practical Applications and Real-World Scenarios
The ability to solve equations like "80% of C is 20" extends far beyond abstract mathematical exercises. These types of calculations are fundamental in numerous real-world applications:
-
Business and Finance: Calculating profits, losses, discounts, sales tax, interest rates, and investment returns all involve percentage calculations. For example, if a business reports that 80% of its sales revenue is profit, and the profit is $20,000, you can use this equation to find the total sales revenue (C).
-
Science and Engineering: Many scientific and engineering applications involve percentage changes, error analysis, and data interpretation. For example, if 80% of a sample decays in a certain time, and the remaining amount is 20 grams, you can use this equation to find the initial amount of the sample.
-
Everyday Life: Percentage calculations are common in everyday situations, such as calculating tips in restaurants, determining sale prices, understanding discounts, or tracking progress towards goals. For example, if you've completed 80% of a project and have 20 pages left, this equation helps you determine the total number of pages in the project.
Expanding the Concept: Variations and Extensions
The basic equation can be modified to explore related concepts:
-
Finding the Percentage: If you know the total value (C) and a part of it (20), you can calculate the percentage. For instance, what percentage of 25 is 20? The calculation would be (20/25) * 100 = 80%.
-
Finding the Part: If you know the percentage and the total value, you can find the part. For example, what is 80% of 30? The calculation would be 0.80 * 30 = 24.
-
Complex Scenarios: More complex scenarios might involve multiple percentage changes or combined percentage calculations. For example, a store might offer a 20% discount on an item already marked down by 15%. These problems often require a step-by-step approach, building upon the basic principles discussed above.
Conclusion: Mastering Percentage Calculations
Understanding how to solve the equation "80% of C is 20" is a crucial skill applicable across various disciplines. The methods outlined – direct algebraic manipulation, proportions, and working with fractions – offer multiple pathways to arrive at the correct answer, reinforcing the understanding of fundamental mathematical principles. This problem serves as a foundation for tackling more complex percentage-based calculations encountered in academic, professional, and everyday contexts. By mastering these basic techniques, you enhance your problem-solving abilities and improve your ability to navigate the quantitative aspects of the world around you. Remember to always break down complex problems into smaller, manageable steps and double-check your work to ensure accuracy. The value of understanding percentage calculations extends far beyond a single equation; it's a fundamental skill for critical thinking and effective problem-solving.
Latest Posts
Related Post
Thank you for visiting our website which covers about 80 Of C Is 20 What Is C . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.