85 Of 60 Is What Number
News Co
Mar 30, 2025 · 5 min read
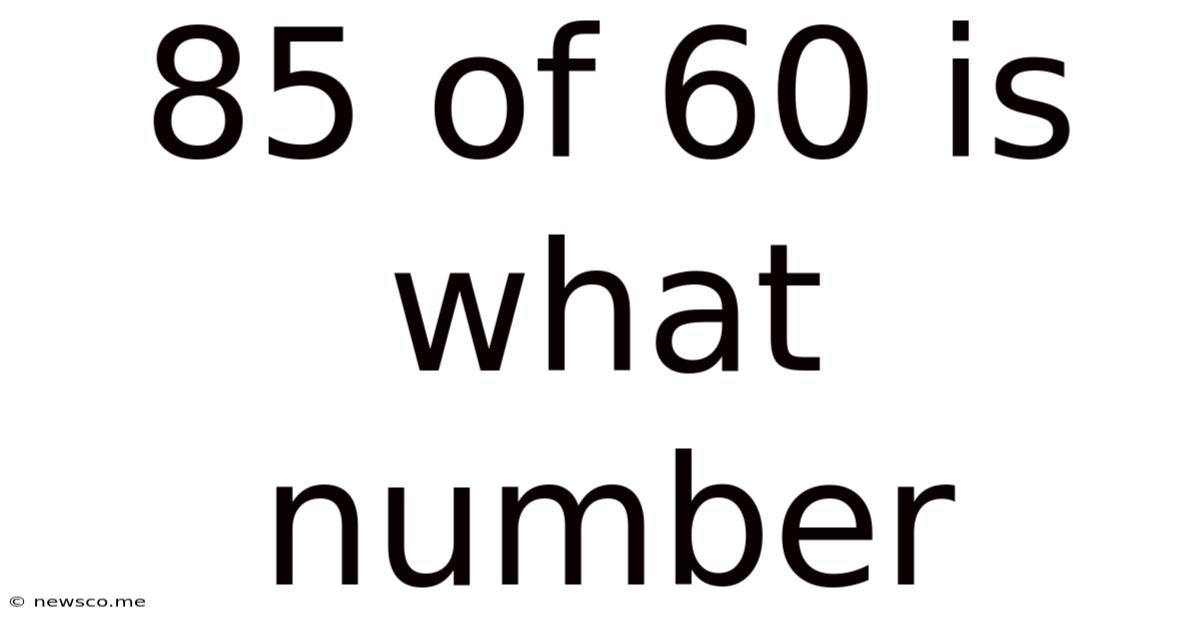
Table of Contents
Decoding Percentages: Understanding "85% of 60 is What Number?"
The question, "85% of 60 is what number?" might seem simple at first glance, but it delves into a fundamental concept in mathematics: percentages. Understanding percentages is crucial in various aspects of life, from calculating discounts and taxes to interpreting statistical data and making informed financial decisions. This comprehensive guide will not only answer the question directly but also explore the underlying principles, providing you with the tools to confidently tackle similar percentage problems.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred" – it represents a portion out of a total of 100 parts. For instance, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5.
Methods to Calculate 85% of 60
There are several ways to calculate 85% of 60. Let's explore the most common approaches:
Method 1: Converting Percentage to Decimal
This is arguably the most straightforward method. To convert a percentage to a decimal, you divide the percentage by 100. In this case:
85% ÷ 100 = 0.85
Now, multiply the decimal by the number you want to find the percentage of:
0.85 x 60 = 51
Therefore, 85% of 60 is 51.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 85% can be written as 85/100. To calculate 85% of 60, we can set up the equation:
(85/100) x 60
This simplifies to:
(17/20) x 60
Further simplification yields:
17 x 3 = 51
Again, we arrive at the answer: 85% of 60 is 51.
Method 3: Proportion Method
This method uses the concept of proportions. We can set up a proportion:
85/100 = x/60
To solve for x (which represents 85% of 60), we cross-multiply:
85 x 60 = 100x
5100 = 100x
x = 5100/100
x = 51
Therefore, 85% of 60 is 51.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in a wide array of real-world scenarios. Here are some examples:
-
Calculating Discounts: If a store offers a 20% discount on an item priced at $100, you would calculate 20% of $100 (0.20 x $100 = $20) to determine the discount amount. The final price would be $100 - $20 = $80.
-
Determining Taxes: Sales tax is usually expressed as a percentage. If the sales tax is 6%, you would calculate 6% of the item's price to determine the tax amount and add it to the original price to get the total cost.
-
Analyzing Financial Statements: Financial statements, such as income statements and balance sheets, frequently use percentages to present data in a more understandable format. For example, profit margins are often expressed as a percentage of revenue.
-
Understanding Statistics: Percentages are ubiquitous in statistics. For example, survey results are often presented as percentages, allowing for easy comparison and interpretation. Polling data showing 60% support for a candidate means that out of 100 people surveyed, 60 expressed support.
-
Calculating Interest: Compound interest calculations heavily rely on percentages. Understanding this helps you understand how your savings grow (or debts accumulate) over time.
-
Grading Systems: Many educational systems use percentages to represent grades. A student scoring 85% on a test means they answered 85 out of 100 questions correctly.
-
Tip Calculations: When dining out, calculating a tip as a percentage of the bill is standard practice. A 15% tip on a $50 bill would be 0.15 x $50 = $7.50.
Beyond the Basics: More Complex Percentage Problems
While "85% of 60" is a relatively straightforward calculation, the principles involved can be extended to solve more complex percentage problems. For instance:
-
Finding the original amount: If you know the percentage and the resulting value, you can work backward to find the original amount. For example, if 25% of a number is 15, you would solve the equation 0.25x = 15 to find the original number (x).
-
Calculating percentage increase or decrease: This involves determining the percentage change between two values. For instance, if a value increases from 100 to 120, the percentage increase is calculated as [(120 - 100) / 100] x 100% = 20%.
-
Working with multiple percentages: Problems might involve applying multiple percentages consecutively, such as calculating a discount followed by a tax. In such cases, it's crucial to perform the calculations in the correct order.
Mastering Percentages: Tips and Tricks
Here are some helpful tips to improve your proficiency with percentage calculations:
-
Practice Regularly: The more you practice, the more confident and efficient you'll become. Start with simple problems and gradually increase the complexity.
-
Use a Calculator: For more complex calculations or when speed is essential, using a calculator can be highly beneficial.
-
Understand the Underlying Concepts: Don't just memorize formulas; strive to understand the logic behind the calculations. This will help you apply the concepts to various situations.
-
Check Your Work: Always double-check your answers to avoid errors. You can do this by using a different method to solve the problem or by estimating the answer before performing the precise calculation.
-
Utilize Online Resources: Many online resources, including calculators and tutorials, can help you further enhance your understanding of percentages.
Conclusion: The Power of Percentage Understanding
The ability to calculate percentages is a fundamental skill with wide-ranging applications. Understanding the different methods – converting percentages to decimals, using fractions, and applying the proportion method – equips you to tackle a variety of percentage-related problems. By mastering these concepts and practicing regularly, you can confidently apply them to real-world scenarios, making informed decisions in finance, shopping, statistics, and many other areas. Remember, the key to mastering percentages lies in understanding the underlying principles and practicing their application. The seemingly simple question, "85% of 60 is what number?", serves as a gateway to a broader understanding of this vital mathematical concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about 85 Of 60 Is What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.