9 3 1 1/3 Next Number
News Co
Apr 13, 2025 · 5 min read
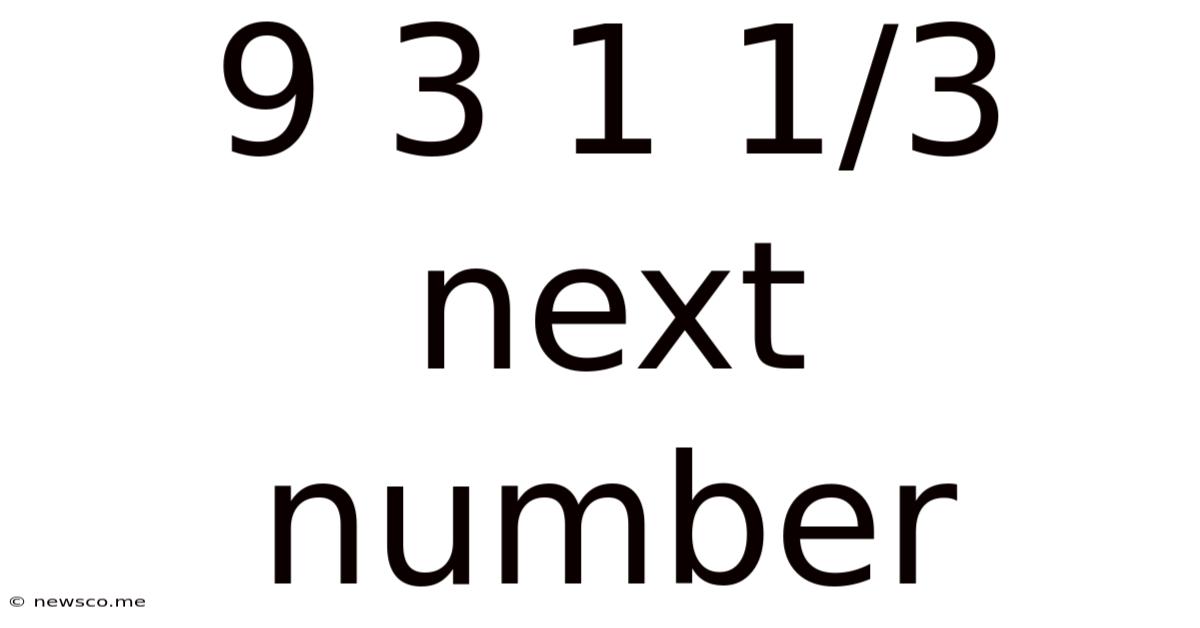
Table of Contents
- 9 3 1 1/3 Next Number
- Table of Contents
- 9, 3, 1, 1/3: Decoding the Next Number in the Sequence
- Identifying the Pattern: A Geometric Progression
- The Formula for a Geometric Progression
- Applying the Formula to Our Sequence
- Alternative Approaches: Exploring Recursive Relationships
- Defining the Recursive Relationship
- Applying the Recursive Relationship
- Visualizing the Sequence: A Graphical Representation
- Extending the Sequence: Exploring Further Terms
- Beyond the Numbers: The Importance of Pattern Recognition
- Practical Applications of Geometric Progressions
- Conclusion: Mastering Mathematical Sequences
- Latest Posts
- Related Post
9, 3, 1, 1/3: Decoding the Next Number in the Sequence
This seemingly simple sequence – 9, 3, 1, 1/3 – presents a fascinating challenge. At first glance, it might appear straightforward, but unraveling the underlying pattern requires a deeper dive into mathematical reasoning. This article will explore various approaches to solving this sequence, explaining the logic behind each method and highlighting the importance of identifying the core mathematical relationship. We'll delve into the concepts of geometric progressions, recursive relationships, and the power of observation in problem-solving. Understanding these methods will equip you with valuable tools for tackling similar numerical puzzles and improve your analytical thinking skills.
Identifying the Pattern: A Geometric Progression
The most evident pattern in the sequence 9, 3, 1, 1/3 is that each subsequent number is obtained by dividing the preceding number by 3. This indicates a geometric progression (GP). A geometric progression is a sequence where each term is obtained by multiplying the previous term by a constant value, known as the common ratio. In this case, the common ratio (r) is 1/3.
The Formula for a Geometric Progression
The general formula for the nth term of a geometric progression is:
a<sub>n</sub> = a<sub>1</sub> * r<sup>(n-1)</sup>
Where:
- a<sub>n</sub> is the nth term of the sequence.
- a<sub>1</sub> is the first term of the sequence.
- r is the common ratio.
- n is the term number.
Applying the Formula to Our Sequence
In our sequence, a<sub>1</sub> = 9 and r = 1/3. Therefore, to find the next number (the 5th term, where n = 5), we apply the formula:
a<sub>5</sub> = 9 * (1/3)<sup>(5-1)</sup> = 9 * (1/3)<sup>4</sup> = 9 * (1/81) = 1/9
Therefore, using the geometric progression method, the next number in the sequence is 1/9.
Alternative Approaches: Exploring Recursive Relationships
While the geometric progression provides a straightforward solution, exploring alternative methods can deepen our understanding of the sequence and enhance our problem-solving skills. We can also analyze this sequence through a recursive relationship. A recursive relationship defines a term in a sequence based on the preceding terms.
Defining the Recursive Relationship
In this case, we can define the recursive relationship as:
a<sub>n</sub> = a<sub>n-1</sub> / 3
This simply states that any term (a<sub>n</sub>) is equal to the previous term (a<sub>n-1</sub>) divided by 3.
Applying the Recursive Relationship
Starting with the last known term, 1/3, we can apply the recursive relationship to find the next term:
a<sub>5</sub> = a<sub>4</sub> / 3 = (1/3) / 3 = 1/9
Again, this method confirms that the next number in the sequence is 1/9.
Visualizing the Sequence: A Graphical Representation
Visualizing the sequence graphically can provide further insights. Plotting the terms on a graph, with the term number on the x-axis and the term value on the y-axis, reveals the exponential decay characteristic of a geometric progression. The graph would show a steadily decreasing curve, approaching zero as the term number increases. This visual representation reinforces the understanding of the sequence's behavior and the nature of the common ratio.
Extending the Sequence: Exploring Further Terms
We can continue extending the sequence using either the geometric progression formula or the recursive relationship. For example, the subsequent terms would be:
- a<sub>6</sub> = (1/9) / 3 = 1/27
- a<sub>7</sub> = (1/27) / 3 = 1/81
- a<sub>8</sub> = (1/81) / 3 = 1/243
- and so on...
This demonstrates the continuous decay towards zero, a hallmark of this type of geometric progression.
Beyond the Numbers: The Importance of Pattern Recognition
Solving this numerical sequence is not merely about finding the next number; it's about developing crucial problem-solving skills. The ability to recognize patterns, whether in mathematics, science, or everyday life, is an invaluable asset. This exercise highlights the significance of:
- Careful observation: Paying close attention to the relationship between numbers is the first step.
- Identifying mathematical concepts: Recognizing the sequence as a geometric progression allows us to apply relevant formulas and methods.
- Using different approaches: Exploring both the geometric progression and recursive methods reinforces understanding and provides a more robust solution.
- Visualizing data: A graphical representation helps visualize the behavior of the sequence and its implications.
Practical Applications of Geometric Progressions
Understanding geometric progressions extends beyond solving mathematical puzzles. They have practical applications in various fields, including:
- Finance: Calculating compound interest, loan repayments, and investment growth often involves geometric progressions.
- Physics: Modeling exponential decay in radioactive materials or the cooling of objects uses geometric progressions.
- Biology: Modeling population growth or the spread of diseases can involve geometric progressions (although often modified to account for limiting factors).
- Computer Science: Analyzing algorithms and data structures sometimes involves geometric progressions.
Conclusion: Mastering Mathematical Sequences
The seemingly simple sequence 9, 3, 1, 1/3 provides a valuable opportunity to practice and enhance mathematical problem-solving skills. By understanding the underlying pattern, applying relevant formulas, and exploring different approaches, we can confidently determine the next number in the sequence as 1/9. Moreover, the exercise demonstrates the importance of pattern recognition, mathematical reasoning, and the diverse applications of geometric progressions in various fields. This analytical approach is applicable to countless other mathematical problems and strengthens our overall problem-solving capabilities. The ability to dissect a problem, identify the core mathematical relationship, and apply the correct tools is a skill that extends far beyond the realm of mathematics itself.
Latest Posts
Related Post
Thank you for visiting our website which covers about 9 3 1 1/3 Next Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.