9 Divided By 5 As A Fraction
News Co
May 02, 2025 · 5 min read
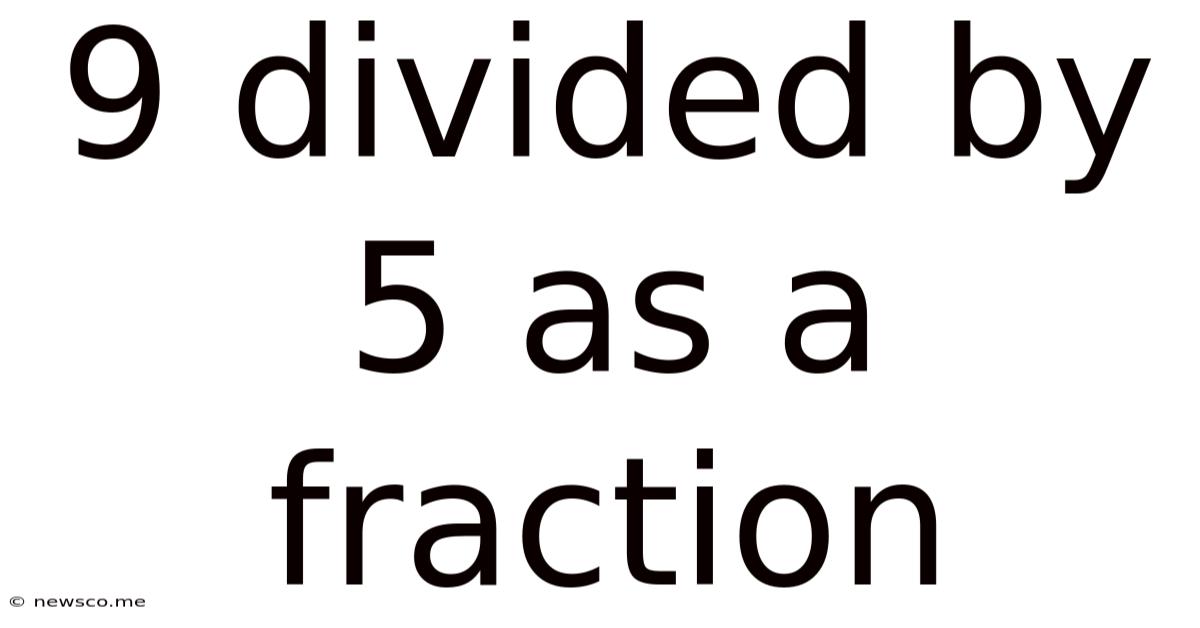
Table of Contents
9 Divided by 5 as a Fraction: A Comprehensive Guide
Understanding fractions is a cornerstone of mathematics, forming the basis for more advanced concepts. This in-depth guide will explore the seemingly simple operation of dividing 9 by 5 and expressing the result as a fraction, delving into the process, different representations, and real-world applications. We'll also touch upon related concepts to provide a complete understanding.
Understanding Division and Fractions
Before diving into the specific problem, let's solidify our understanding of division and fractions. Division is essentially the process of splitting a quantity into equal parts. For example, dividing 10 by 2 means splitting 10 into two equal groups of 5.
Fractions, on the other hand, represent parts of a whole. They have a numerator (the top number) representing the number of parts we have, and a denominator (the bottom number) representing the total number of equal parts the whole is divided into. For example, ½ represents one out of two equal parts.
Expressing 9 Divided by 5 as a Fraction
The problem "9 divided by 5" can be written as 9 ÷ 5. To express this as a fraction, we simply write the dividend (the number being divided) as the numerator and the divisor (the number we're dividing by) as the denominator. Therefore, 9 divided by 5 as a fraction is:
9/5
This fraction is an improper fraction because the numerator (9) is larger than the denominator (5). Improper fractions are perfectly valid mathematical expressions, but they can often be converted into other forms for better understanding or easier calculations.
Converting the Improper Fraction to a Mixed Number
An improper fraction can be converted into a mixed number, which combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). To do this, we perform the division:
9 ÷ 5 = 1 with a remainder of 4.
The whole number part of the mixed number is the quotient (1). The fractional part is the remainder (4) over the divisor (5). Therefore, 9/5 as a mixed number is:
1 ⅘
This means we have one whole and four-fifths of another.
Decimal Representation
Fractions can also be represented as decimals. To convert 9/5 to a decimal, we simply perform the division:
9 ÷ 5 = 1.8
So, 9/5 is equivalent to 1.8.
Visual Representation
Visualizing fractions can be helpful, especially for grasping the concept. Imagine a rectangle divided into 5 equal parts. Shading 9 of these parts would represent the fraction 9/5. This visually demonstrates the improper fraction – we have more shaded parts than the total number of parts in a single whole rectangle. You would need two rectangles to fully represent the fraction.
Real-World Applications
Understanding how to express 9/5 in different forms has practical applications in various situations:
- Baking: If a recipe calls for 9/5 cups of flour, you would know to use 1 and ⅘ cups.
- Measurements: If you measure 9/5 meters of fabric, you would understand that it is equivalent to 1.8 meters.
- Sharing: If you need to divide 9 apples among 5 people, each person gets 9/5 or 1 ⅘ apples.
Equivalent Fractions
It's crucial to understand that a fraction can have many equivalent forms. To find an equivalent fraction, you simply multiply or divide both the numerator and the denominator by the same non-zero number. For example:
- 9/5 is equivalent to 18/10 (multiplying both by 2)
- 9/5 is equivalent to 27/15 (multiplying both by 3)
- 9/5 is equivalent to 45/25 (multiplying both by 5)
All these fractions represent the same quantity.
Adding and Subtracting Fractions
Understanding fractions is key to performing operations with them. To add or subtract fractions, they must have the same denominator (a common denominator). If they don't, you need to find one. Let's say we want to add 9/5 and 2/5:
9/5 + 2/5 = (9+2)/5 = 11/5 = 2 ⅕
If the denominators are different, for example, adding 9/5 and 1/2, we need to find a common denominator (in this case, 10):
9/5 = 18/10 1/2 = 5/10
18/10 + 5/10 = 23/10 = 2 ⅗
Multiplying and Dividing Fractions
Multiplying fractions is relatively straightforward; you multiply the numerators together and the denominators together. Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying.
Multiplication:
(9/5) * (2/3) = (92)/(53) = 18/15 = 6/5 = 1 ⅕
Division:
(9/5) ÷ (2/3) = (9/5) * (3/2) = (93)/(52) = 27/10 = 2 ⅞
Simplifying Fractions
Simplifying a fraction means reducing it to its lowest terms. This is done by finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it. For example, simplifying 18/15:
The GCD of 18 and 15 is 3.
18 ÷ 3 = 6 15 ÷ 3 = 5
Therefore, 18/15 simplifies to 6/5.
Conclusion
The seemingly simple operation of dividing 9 by 5 opens a window into the world of fractions, revealing their multiple representations and practical applications. Understanding improper fractions, mixed numbers, decimals, equivalent fractions, and the ability to perform operations with fractions are fundamental skills with far-reaching implications across various mathematical and real-world contexts. By mastering these concepts, you build a strong foundation for tackling more advanced mathematical challenges. Remember to practice regularly to solidify your understanding and enhance your problem-solving abilities. The more you work with fractions, the more intuitive they become!
Latest Posts
Related Post
Thank you for visiting our website which covers about 9 Divided By 5 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.