A Cube Plus B Cube Plus C Cube Ka Sutra
News Co
May 07, 2025 · 5 min read
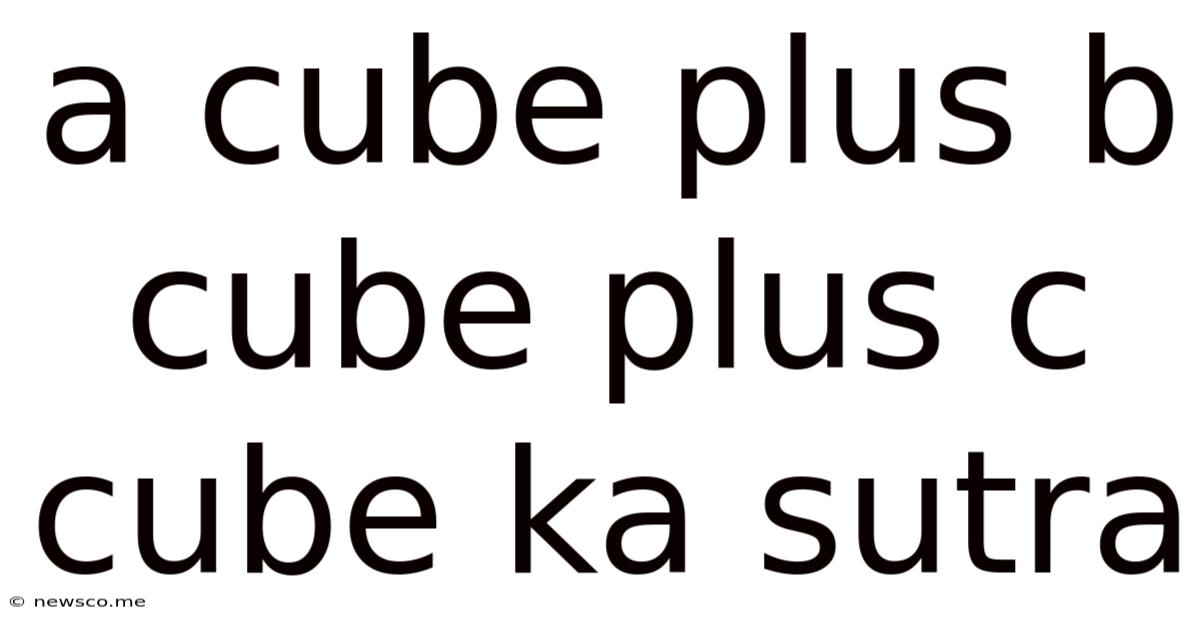
Table of Contents
A Cube Plus B Cube Plus C Cube Ka Sutra: Exploring the Mathematical Identity and its Applications
The algebraic identity, often referred to as "a cube plus b cube plus c cube ka sutra" in Hindi, represents the expansion of the expression (a + b + c)³ – 3(a + b)(b + c)(c + a). While there isn't a single, universally accepted "sutra" (formula) in the traditional sense for this specific expansion, understanding this identity and its relationship to the sum of cubes is crucial in various mathematical fields. This article will delve deep into this identity, exploring its derivation, applications, and significance in different mathematical contexts.
Understanding the Identity: (a + b + c)³ – 3(a + b)(b + c)(c + a)
The core of the problem lies in expanding the expression (a + b + c)³. While there isn't a direct, concise formula like a² + b² for the sum of squares, we can derive a useful identity. Let's break it down systematically:
Step-by-Step Expansion of (a + b + c)³
-
Initial Expansion: We begin by expanding (a + b + c)³ as (a + b + c)(a + b + c)(a + b + c). This involves a significant amount of multiplication.
-
Systematic Multiplication: To avoid errors, a methodical approach is needed. We can use the distributive property repeatedly, expanding the expression term by term. This process will yield terms involving a³, b³, c³, a²b, a²c, ab², ac², b²c, bc², and abc.
-
Collecting Like Terms: After completing the multiplication, we meticulously collect and combine similar terms (e.g., all the terms with a²b will be added together). This simplification is crucial for obtaining the final identity.
-
The Final Result: After the complete expansion and simplification, we arrive at the identity:
(a + b + c)³ = a³ + b³ + c³ + 3(a + b)(b + c)(c + a)
This identity directly relates the cube of the sum of three variables (a, b, and c) to the sum of their individual cubes and an additional term involving their pairwise sums.
Rearranging the Identity to Isolate a³ + b³ + c³
From the identity above, we can easily rearrange the terms to isolate the sum of cubes:
a³ + b³ + c³ = (a + b + c)³ – 3(a + b)(b + c)(c + a)
This form is essential for various applications because it expresses the sum of cubes in terms of the sum of the variables and their pairwise products.
Applications of the Identity
This seemingly simple algebraic identity has far-reaching applications in various mathematical domains:
1. Solving Cubic Equations
While not directly solving cubic equations in their general form, this identity can be a valuable tool in specific cases. If we know the sum (a + b + c) and the pairwise products (ab, bc, ca), we can potentially use this identity to find the individual values of a, b, and c. However, the utility is limited to scenarios with sufficient constraints.
2. Geometric Applications
The identity has interesting geometric interpretations. Consider a cube with sides of length (a + b + c). The identity relates the volume of this large cube to the volumes of smaller cubes and cuboids within it. This relationship can be used to derive geometric proofs or solve specific volume-related problems.
3. Number Theory
This identity finds application in number theory, particularly when dealing with properties of integers. It can help in proving certain number-theoretic statements or identifying special relationships between integers.
4. Advanced Algebraic Manipulations
This identity serves as a building block for more complex algebraic manipulations and proofs. It can be used to simplify expressions, derive new identities, or solve challenging algebraic problems that appear in higher-level mathematics.
Comparing with the Sum of Cubes Formula (a³ + b³ + c³ – 3abc)
It's crucial to differentiate this identity from the related formula for the sum of cubes when a + b + c = 0. In this specific scenario, the identity simplifies dramatically:
If a + b + c = 0, then (a + b + c)³ = 0. Therefore, a³ + b³ + c³ = –3(a + b)(b + c)(c + a) = 3abc
This special case is often presented as a separate formula:
If a + b + c = 0, then a³ + b³ + c³ = 3abc
This simplified form is remarkably useful in solving certain algebraic problems and proving specific mathematical results. It showcases the power of exploring special cases within broader identities.
Practical Examples and Exercises
Let’s illustrate the identity’s use with a couple of examples:
Example 1: Find the value of a³ + b³ + c³ if a = 2, b = 3, and c = -5.
Using the identity: a³ + b³ + c³ = (a + b + c)³ – 3(a + b)(b + c)(c + a)
Substituting the values: a + b + c = 2 + 3 + (-5) = 0 Therefore, a³ + b³ + c³ = 3abc = 3(2)(3)(-5) = -90
Example 2: Verify the identity for a = 1, b = 2, c = 3.
-
Calculate (a + b + c)³: (1 + 2 + 3)³ = 6³ = 216
-
Calculate a³ + b³ + c³: 1³ + 2³ + 3³ = 1 + 8 + 27 = 36
-
Calculate 3(a + b)(b + c)(c + a): 3(1 + 2)(2 + 3)(3 + 1) = 3(3)(5)(4) = 180
-
Verify the identity: 36 + 180 = 216. The identity holds true.
Conclusion: The Importance of Understanding a Cube Plus B Cube Plus C Cube Ka Sutra
The identity discussed, though not a single concise "sutra" in the traditional sense, represents a powerful tool in algebra. Understanding its derivation and applications across different mathematical areas is vital for students and mathematicians alike. Its ability to relate the cube of a sum to the sum of cubes, particularly the special case when the sum is zero, provides valuable insights and facilitates the solution of numerous algebraic problems. While it might not be explicitly named as a single "sutra," its importance in algebraic manipulation and problem-solving is undeniable. Mastering this identity strengthens one's algebraic skills and opens doors to tackling more complex mathematical concepts. Remember that the key is understanding the underlying principles, not just memorizing formulas.
Latest Posts
Related Post
Thank you for visiting our website which covers about A Cube Plus B Cube Plus C Cube Ka Sutra . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.