A Parallelogram With Four Congruent Sides
News Co
Apr 06, 2025 · 6 min read
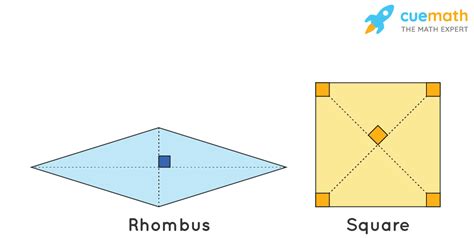
Table of Contents
A Parallelogram with Four Congruent Sides: Exploring the Properties of a Rhombus
A parallelogram, a fundamental geometric shape, is defined by its parallel opposite sides. But what happens when we add a constraint – what if all four sides are congruent (equal in length)? This special type of parallelogram is known as a rhombus. This article delves deep into the fascinating properties of a rhombus, exploring its geometric characteristics, its relationship to other quadrilaterals, and its various applications in mathematics and beyond. We'll explore everything from its simple definition to its complex applications in fields like vector mathematics and crystallography.
Defining the Rhombus: More Than Just Equal Sides
A rhombus is a quadrilateral (a four-sided polygon) with all four sides having equal length. This simple definition unlocks a surprising array of unique properties. Because a rhombus is a parallelogram, it inherits all the properties of a parallelogram:
- Opposite sides are parallel: This fundamental property is the cornerstone of the parallelogram, and thus, the rhombus.
- Opposite angles are equal: The angles opposite each other within a rhombus are congruent.
- Consecutive angles are supplementary: Any two angles adjacent to each other add up to 180 degrees.
- Diagonals bisect each other: The diagonals intersect at their midpoints, dividing each other into two equal segments.
However, the rhombus possesses additional properties not shared by all parallelograms, making it a distinctly interesting geometric figure.
Unique Properties of a Rhombus
The equal side lengths of a rhombus lead to several distinctive characteristics:
- Diagonals are perpendicular bisectors: This is a crucial difference. The diagonals of a rhombus not only bisect each other but also intersect at a right angle (90 degrees). This perpendicularity is a defining feature and a powerful tool for solving problems related to rhombuses.
- Diagonals bisect the angles: Each diagonal of a rhombus bisects a pair of opposite angles. This means each diagonal divides its corresponding angles into two equal halves.
- Symmetry: A rhombus exhibits both rotational and reflectional symmetry. It has rotational symmetry of order 2 (180-degree rotation) and two lines of reflectional symmetry (along its diagonals).
Rhombus vs. Other Quadrilaterals: A Comparative Analysis
Understanding the rhombus requires comparing it to other quadrilaterals sharing some, but not all, of its properties. Let's explore these relationships:
Rhombus vs. Parallelogram
As mentioned earlier, a rhombus is a special case of a parallelogram. All rhombuses are parallelograms, but not all parallelograms are rhombuses. The key difference lies in the side lengths: a parallelogram only requires opposite sides to be equal; a rhombus demands all sides to be equal.
Rhombus vs. Square
A square is a special type of rhombus. A square is a rhombus with the additional constraint that all its angles are right angles (90 degrees). Therefore, every square is a rhombus, but not every rhombus is a square. The distinction is subtle yet crucial.
Rhombus vs. Rectangle
A rectangle is a parallelogram with all angles equal to 90 degrees. A rhombus and a rectangle do not directly overlap except in the case of a square. A rhombus can have angles other than 90 degrees, while a rectangle must have all angles at 90 degrees.
Rhombus vs. Kite
A kite is a quadrilateral with two pairs of adjacent sides that are congruent. While both kites and rhombuses have pairs of equal sides, the arrangement differs. In a kite, the equal sides are adjacent, whereas in a rhombus, they are opposite. A rhombus can be considered a special type of kite where all sides are equal.
Calculating Area and Perimeter of a Rhombus
The area and perimeter of a rhombus can be calculated using different formulas depending on the available information.
Perimeter of a Rhombus
Since all four sides of a rhombus are equal in length (let's denote this length as 'a'), the perimeter (P) is simply:
P = 4a
This formula is straightforward and requires only the length of one side.
Area of a Rhombus: Multiple Approaches
Calculating the area of a rhombus offers more flexibility. Here are some common methods:
- Using base and height: Similar to a parallelogram, the area (A) can be calculated using the base (b) and height (h):
A = bh
- Using diagonals: This method leverages the perpendicular diagonals. If the lengths of the diagonals are 'd1' and 'd2', then the area is:
A = (1/2) * d1 * d2
This formula is particularly useful when the base and height aren't directly known but the diagonal lengths are available.
- Using trigonometry: If one side length ('a') and one angle ('θ') are known, the area can be calculated using:
A = a² * sin(θ)
Applications of Rhombuses: From Geometry to Real World
Rhombuses, while seemingly simple shapes, appear surprisingly often in various fields:
Geometry and Mathematics
- Tessellations: Rhombuses, along with other shapes, can be used to create tessellations – patterns that cover a plane without gaps or overlaps. This is frequently explored in both artistic and mathematical contexts.
- Vector Mathematics: Rhombuses provide a visual representation of vector addition and subtraction. The diagonals represent the vectors, and their lengths and orientations offer a practical way to understand vector operations.
- Coordinate Geometry: Understanding rhombuses is essential for solving problems involving coordinate systems and geometric transformations.
Real-World Examples
- Crystals: Many crystals have rhombic structures, reflecting the inherent symmetry and geometric stability of the shape.
- Art and Design: The visual appeal of rhombuses has led to their incorporation into various forms of art, architecture, and design. From stained glass windows to modern art installations, the rhombus adds a unique aesthetic element.
- Engineering: Rhombus-shaped structures are sometimes used in engineering designs, particularly where strength and stability are required. The shape can efficiently distribute stress.
- Kites: Many kites are essentially rhombuses (or close approximations thereof) in their design.
Advanced Properties and Theorems Related to Rhombuses
Exploring rhombuses further involves understanding more sophisticated concepts and theorems:
Brahmagupta's Formula (for cyclic quadrilaterals):
While a rhombus is not always cyclic (meaning its vertices don't lie on a circle), understanding Brahmagupta's formula for the area of cyclic quadrilaterals offers a broader mathematical context. This is especially relevant if considering a specific type of rhombus (a square, which is cyclic).
Relationship to Complex Numbers:
Representing the vertices of a rhombus using complex numbers can lead to elegant solutions for various problems involving their properties. This approach often simplifies calculations and provides deeper insights.
Applications in Linear Algebra:
Rhombuses can be used to illustrate concepts in linear algebra, specifically related to matrices and transformations.
Conclusion: The Unsung Hero of Geometry
The rhombus, despite its simplicity, is a rich and versatile geometric shape. Its unique properties, its relationship to other quadrilaterals, and its wide range of applications highlight its importance in mathematics and beyond. From the intricacies of crystallography to the artistic beauty of tessellations, the rhombus continues to fascinate and inspire, reminding us that even the simplest shapes can hold profound mathematical significance and practical relevance. Further exploration into its properties will undoubtedly reveal even more hidden depths within this seemingly straightforward geometric form.
Latest Posts
Related Post
Thank you for visiting our website which covers about A Parallelogram With Four Congruent Sides . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.