A Rhombus Is ____ A Quadrilateral.
News Co
May 09, 2025 · 6 min read
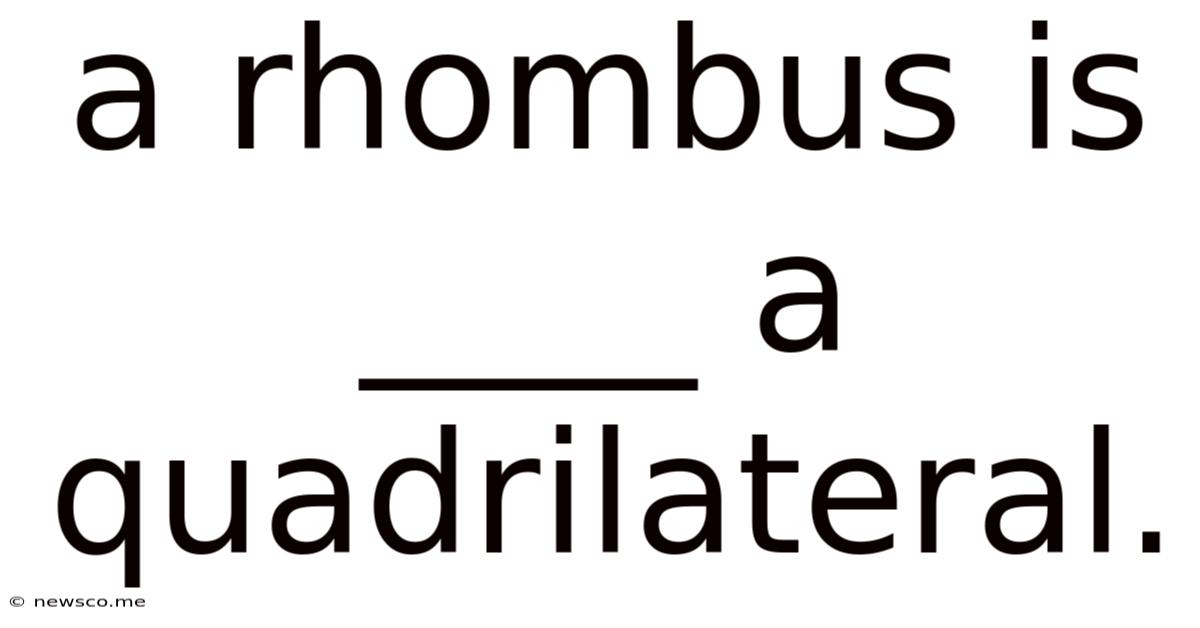
Table of Contents
A Rhombus Is a Special Kind of Quadrilateral
A rhombus is a quadrilateral, but not just any quadrilateral. It's a special type, possessing unique properties that distinguish it from other four-sided shapes like squares, rectangles, trapezoids, and parallelograms. Understanding these properties is key to grasping the rhombus's place within the broader family of quadrilaterals. This article will delve deep into the definition, properties, and applications of the rhombus, exploring its geometric intricacies and solidifying your understanding of this fascinating shape.
Defining the Rhombus: More Than Just a Quadrilateral
Let's start with the basics. A quadrilateral is simply any polygon with four sides. This is a broad category encompassing a wide variety of shapes. A rhombus, however, is a more specific type of quadrilateral. It’s defined as a quadrilateral with all four sides of equal length. This simple definition sets it apart from many other quadrilaterals. Think of it as a "supercharged" parallelogram, inheriting many of its properties but with the added constraint of equal side lengths.
Distinguishing the Rhombus from Other Quadrilaterals
It's crucial to understand how the rhombus differs from other quadrilaterals:
-
Square: A square is a special case of a rhombus. It satisfies all the conditions of a rhombus (equal side lengths) and has four right angles. Therefore, a square is a rhombus, but a rhombus is not necessarily a square.
-
Rectangle: A rectangle is another quadrilateral with four right angles, but its sides are not necessarily equal in length. Therefore, a rectangle is not a rhombus.
-
Parallelogram: A parallelogram is a quadrilateral with two pairs of parallel sides. A rhombus is a parallelogram because its equal side lengths ensure parallel opposite sides. However, not all parallelograms are rhombuses, as parallelograms don't necessarily have all four sides of equal length.
-
Trapezoid (or Trapezium): A trapezoid has at least one pair of parallel sides. A rhombus, with its two pairs of parallel sides, is not a trapezoid unless it's a degenerate case.
-
Kite: A kite has two pairs of adjacent sides that are equal in length. While a rhombus shares this property (though it also has two pairs of equal opposite sides), a kite does not necessarily have all four sides equal.
In summary, the rhombus occupies a specific niche within the hierarchy of quadrilaterals. It’s a more specialized shape compared to a general quadrilateral, sharing properties with parallelograms but possessing the distinct characteristic of having all sides equal in length.
Key Properties of a Rhombus: A Deeper Dive
Beyond the basic definition, the rhombus boasts several remarkable properties that make it a rich subject of geometric study:
1. All Sides are Equal
This is the defining characteristic of a rhombus. Each of its four sides is congruent (equal in length). This property underlies many of the other properties that follow.
2. Opposite Sides are Parallel
Like all parallelograms, a rhombus has two pairs of parallel sides. This parallelism is a direct consequence of the equal side lengths. Opposite sides are not only equal in length but also parallel to each other.
3. Opposite Angles are Equal
The opposite angles of a rhombus are congruent. This means they have the same measure. This property stems from the parallelogram property and the equal side lengths reinforcing the symmetry.
4. Consecutive Angles are Supplementary
Consecutive angles (angles next to each other) in a rhombus are supplementary, meaning their measures add up to 180 degrees. This property again is a consequence of the parallel sides.
5. Diagonals Bisect Each Other
The diagonals of a rhombus (the line segments connecting opposite vertices) intersect at a point that bisects each diagonal. This means each diagonal is cut into two equal parts by the other.
6. Diagonals are Perpendicular Bisectors
Not only do the diagonals bisect each other, but they also intersect at right angles (90 degrees). This perpendicularity is a unique characteristic that distinguishes rhombuses from other parallelograms.
7. Diagonals Bisect the Angles
Each diagonal of a rhombus bisects a pair of opposite angles. This means it divides each angle into two equal angles.
These properties are interconnected and form a coherent set of characteristics that define and distinguish a rhombus. Understanding these properties allows for various geometric calculations and constructions related to the rhombus.
Applications of Rhombuses: Beyond Geometry
Rhombuses are not just abstract geometric shapes; they appear in numerous real-world applications and contexts:
1. Engineering and Construction
Rhombus shapes are frequently used in engineering and construction for their structural strength and stability. Think of the supporting structures in bridges or the patterns in certain architectural designs. The equal side lengths and parallel sides provide stability and distribute forces effectively.
2. Design and Art
Rhombuses are used extensively in design and art, contributing to visually appealing patterns and textures. They create a dynamic and visually engaging aesthetic that is used in various forms, from textile designs to modern art.
3. Crystallography
In crystallography, the rhombus plays a significant role in understanding the structure and arrangement of atoms and molecules in crystalline materials. Certain crystal structures exhibit rhombic arrangements.
4. Games and Puzzles
Rhombuses also feature in various games and puzzles. They can be components of tessellations (tilings that cover a surface without overlapping), creating intricate and beautiful patterns.
5. Nature
Remarkably, rhombus shapes can even be observed in nature, such as in some crystal formations or arrangements of leaves and petals.
Calculating Area and Perimeter of a Rhombus: Practical Applications
The properties of a rhombus lend themselves to straightforward calculations of its area and perimeter.
Calculating the Perimeter
The perimeter of a rhombus is simply the sum of the lengths of its four sides. Since all sides are equal, the perimeter (P) is given by:
P = 4s, where 's' is the length of one side.
Calculating the Area
The area of a rhombus can be calculated in a few ways:
-
Using the side length and height: Area (A) = base * height = s * h, where 's' is the length of a side and 'h' is the perpendicular height from one side to the opposite side.
-
Using the diagonals: Area (A) = (1/2)d₁d₂, where d₁ and d₂ are the lengths of the two diagonals. This formula is particularly useful as the diagonals are often readily measurable.
These formulas allow for practical calculations of the area and perimeter, which are vital in various applications, from determining the amount of material needed in construction to calculating the surface area of certain crystalline structures.
Conclusion: The Rhombus – A Unique and Useful Quadrilateral
In conclusion, a rhombus is a unique and fascinating quadrilateral distinguished by its equal side lengths and the properties that stem from this characteristic. Its properties, including parallel opposite sides, congruent opposite angles, and perpendicular bisecting diagonals, make it a rich subject of geometric study and a valuable shape in various practical applications. From engineering to art and crystallography, the rhombus demonstrates the power and beauty of geometric principles in the real world. Understanding its properties is essential for anyone interested in geometry, design, or the broader applications of mathematical principles. The rhombus stands as a testament to the elegance and utility of this special kind of quadrilateral within the larger world of shapes and forms.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about A Rhombus Is ____ A Quadrilateral. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.