Ab And Cd Intersect At Point O As Shown Below
News Co
Apr 06, 2025 · 5 min read
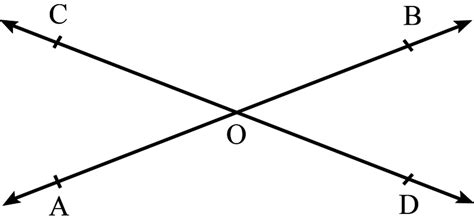
Table of Contents
AB and CD Intersect at Point O: A Comprehensive Exploration of Geometry
This article delves into the geometrical relationships arising when two lines, AB and CD, intersect at a point O. We'll explore various concepts, theorems, and applications related to this fundamental scenario in geometry. We'll cover topics ranging from basic angle relationships to more advanced concepts, ensuring a thorough understanding for students and enthusiasts alike.
Understanding the Intersection: Basic Angle Relationships
When two lines intersect, they form four angles. In our case, lines AB and CD intersect at point O, creating angles ∠AOC, ∠COB, ∠BOD, and ∠DOA. These angles possess specific relationships, crucial for solving numerous geometric problems.
Vertically Opposite Angles: Equality in Symmetry
Vertically opposite angles are angles that are opposite each other when two lines intersect. In our scenario, ∠AOC and ∠BOD are vertically opposite, as are ∠COB and ∠DOA. A fundamental theorem states that vertically opposite angles are always equal. This means:
- ∠AOC = ∠BOD
- ∠COB = ∠DOA
This property is incredibly useful in solving problems involving intersecting lines. Understanding this equality allows for the simplification of complex geometric figures and the derivation of unknown angle measurements.
Linear Pairs: Supplementary Angles on a Straight Line
A linear pair consists of two adjacent angles that form a straight line. In our diagram, the following are linear pairs:
- ∠AOC and ∠COB
- ∠COB and ∠BOD
- ∠BOD and ∠DOA
- ∠DOA and ∠AOC
Adjacent angles in a linear pair are supplementary, meaning their sum is always 180°. This is because a straight line represents an angle of 180°. Therefore:
- ∠AOC + ∠COB = 180°
- ∠COB + ∠BOD = 180°
- ∠BOD + ∠DOA = 180°
- ∠DOA + ∠AOC = 180°
This supplementary relationship is another cornerstone of solving problems involving intersecting lines. It allows for the calculation of one angle if the other angle in the linear pair is known.
Beyond Basic Relationships: Exploring Further Applications
The intersection of AB and CD at point O opens up avenues for exploring more intricate geometrical concepts and their practical applications.
Angle Bisectors and Their Properties
An angle bisector is a line segment that divides an angle into two equal angles. If we introduce angle bisectors for any of the four angles formed by the intersection, new relationships emerge. For instance, if we bisect ∠AOC, creating a ray OE, then ∠AOE = ∠COE = ½∠AOC. These bisectors can create further relationships between other angles within the figure, allowing for more complex problem-solving.
Perpendicular Lines and Right Angles
If lines AB and CD are perpendicular (intersect at a right angle), then all four angles formed are right angles (90°). This special case simplifies calculations significantly, as all angles are known. Perpendicular lines are frequently encountered in various geometrical constructions and real-world applications such as building construction and map-making.
Introducing Transversals: Parallel Lines and Their Implications
When a third line intersects AB and CD (acting as a transversal), the scenario becomes even richer. If AB and CD are parallel, specific angle relationships emerge:
- Alternate Interior Angles: These are equal (e.g., angles formed between AB and CD on opposite sides of the transversal).
- Alternate Exterior Angles: These are also equal (e.g., angles formed outside AB and CD on opposite sides of the transversal).
- Corresponding Angles: These are equal (angles in the same relative position with respect to AB, CD, and the transversal).
- Consecutive Interior Angles: These are supplementary (angles between AB and CD on the same side of the transversal).
These relationships are crucial in proving lines are parallel or finding unknown angles when parallelism is established. This concept forms a significant part of Euclidean geometry and is vital in various branches of mathematics and engineering.
Real-World Applications and Problem-Solving
The seemingly simple intersection of two lines has widespread applications across various disciplines:
Surveying and Mapping:
Surveyors use the principles of intersecting lines to determine distances and angles, crucial in creating accurate maps and land surveys. Understanding angle relationships allows them to calculate unknown measurements based on known values.
Construction and Engineering:
In construction and engineering, accurate angle measurements are paramount. The intersection of lines, along with principles of parallel and perpendicular lines, guides the design and construction of buildings, bridges, and other structures.
Computer Graphics and Game Development:
In computer graphics and game development, the concept of intersecting lines is fundamental. It is used to determine collisions between objects, create realistic rendering of scenes, and simulate physics in virtual environments.
Advanced Concepts and Extensions
The intersection of lines AB and CD can serve as a foundation for more advanced geometrical explorations:
Coordinate Geometry:
In coordinate geometry, the intersection point O can be expressed as a pair of coordinates (x, y). Using equations of lines AB and CD, we can find the coordinates of O by solving a system of linear equations. This allows for analytical solutions and manipulations of geometric figures using algebraic techniques.
Vectors and Linear Algebra:
Vector representation of lines AB and CD allows for a more abstract and powerful way to analyze their intersection. The intersection point can be found through vector operations and linear algebra techniques. This approach provides insights into the geometric properties of lines and their intersections.
Projective Geometry:
Projective geometry extends the concepts of lines and intersections to a broader framework. It deals with properties that are invariant under projective transformations, offering a powerful tool to analyze perspective and transformations in geometric figures.
Conclusion: A Foundation for Deeper Understanding
The intersection of lines AB and CD at point O, while seemingly simple, provides a rich foundation for exploring fundamental geometric principles. Understanding the relationships between angles, including vertically opposite angles, linear pairs, and the implications of parallel lines and transversals, is crucial for solving various geometric problems. Furthermore, extending these concepts to coordinate geometry, vectors, and projective geometry unlocks powerful analytical and abstract tools for a deeper appreciation of geometry. This seemingly simple intersection is indeed a cornerstone of geometric understanding and has widespread applications in diverse fields. Mastering these concepts is essential for success in mathematics, engineering, and other related disciplines.
Latest Posts
Related Post
Thank you for visiting our website which covers about Ab And Cd Intersect At Point O As Shown Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.