All Positive Even Numbers Less Than 10
News Co
May 08, 2025 · 5 min read
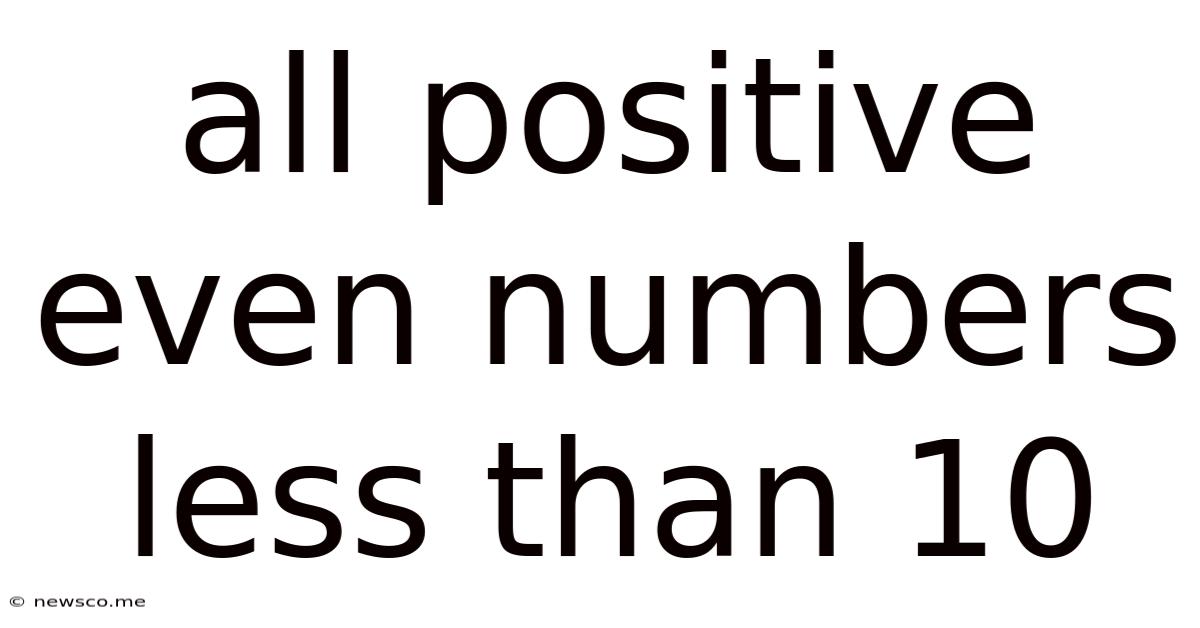
Table of Contents
All Positive Even Numbers Less Than 10: A Deep Dive into a Simple Set
The seemingly trivial question, "What are all positive even numbers less than 10?" opens a door to exploring fundamental mathematical concepts, their applications, and even their representation in computer science. While the answer itself is straightforward – 2, 4, 6, and 8 – the journey to understanding this simple set reveals a surprising depth. This article will delve into this seemingly simple set, exploring its properties, its significance in various fields, and its representation in different contexts.
Understanding Even Numbers
Before we delve into the specifics of our set, let's establish a firm understanding of what constitutes an even number. An even number is any integer that is perfectly divisible by 2, leaving no remainder. This means that it can be expressed in the form 2n, where 'n' is any integer. Zero is considered an even number because it satisfies this condition (2 * 0 = 0). Negative even numbers also exist (-2, -4, -6, etc.), but our focus here is exclusively on positive even numbers less than 10.
The Set {2, 4, 6, 8}
Our target set, {2, 4, 6, 8}, is a finite set containing only four elements. Its simplicity belies the richness of mathematical concepts that can be illustrated using it. We can analyze this set from various perspectives:
-
Arithmetic Properties: Each element is divisible by 2. They also exhibit properties related to addition, subtraction, and multiplication. For instance, the sum of any two elements in the set is an even number. The product of any two elements is also an even number. These properties are not coincidental; they are direct consequences of the definition of even numbers.
-
Set Theory: This set can be formally described using set notation: {x | x ∈ ℤ⁺, x < 10, x mod 2 = 0}. This notation reads as "the set of all x such that x is a positive integer (ℤ⁺), x is less than 10, and x modulo 2 is equal to 0 (meaning it's divisible by 2)." This showcases how set theory provides a precise and concise way to define collections of elements.
-
Number Systems: The elements of this set can be represented in different number systems. For example, in binary (base-2), they are 10, 100, 110, and 1000. In hexadecimal (base-16), they are 2, 4, 6, and 8, the same as in decimal (base-10). Understanding different number systems is crucial in computer science and other fields that deal with data representation.
Applications and Significance
While seemingly simple, the set {2, 4, 6, 8} appears in various contexts, highlighting its importance:
Elementary Mathematics
This set is fundamental to teaching basic arithmetic operations to children. Learning to add, subtract, multiply, and divide these numbers lays the foundation for more complex mathematical concepts. Understanding even numbers is crucial for grasping concepts like divisibility rules and prime factorization.
Computer Science
In programming, representing and manipulating even numbers is commonplace. Many algorithms rely on even/odd number distinctions. For example:
-
Bit Manipulation: Checking if a number is even can be done efficiently by examining its least significant bit (LSB). If the LSB is 0, the number is even; otherwise, it is odd. This bitwise operation is computationally very fast.
-
Looping and Iteration: Even numbers are frequently used in loop control structures. For example, iterating through an array with even indices can be optimized using even numbers in the loop condition.
-
Data Structures: Certain data structures, such as linked lists or trees, might employ even or odd addressing schemes for improved efficiency or specific functionalities.
Number Theory
Even numbers are central to many concepts in number theory. For example:
-
Goldbach's Conjecture: This famous unsolved problem in number theory postulates that every even integer greater than 2 can be expressed as the sum of two prime numbers. While not directly related to our set {2, 4, 6, 8}, it highlights the importance of even numbers in prime number distribution studies.
-
Perfect Numbers: A perfect number is a positive integer that is equal to the sum of its proper divisors (excluding itself). The smallest even perfect number is 6, which is present in our set. The study of perfect numbers is an active area of research in number theory.
Real-World Applications
While less obvious, even numbers have real-world applications:
-
Counting: We use even numbers all the time for counting pairs of items, arranging objects symmetrically, or measuring quantities that come in pairs (e.g., shoes, gloves).
-
Calendar and Time: The number of days in many months are either 30 or 31; only February has an even number of days (28 or 29), emphasizing the presence of even numbers in our time-keeping systems.
Extending the Concept
We can expand upon the initial set {2, 4, 6, 8} by considering various extensions:
Set of all Positive Even Numbers
Expanding our focus to the infinite set of all positive even numbers (denoted as {2, 4, 6, 8, 10, ...}) allows for exploration of concepts like sequences, series, and limits in calculus. This set is an arithmetic progression with a common difference of 2.
Even Numbers within a Larger Range
Considering even numbers within a larger range, such as all even numbers between 1 and 100, or even numbers between 1000 and 2000, allows for the exploration of statistical properties, frequency distributions, and other aspects of data analysis.
Even Numbers and Other Number Sets
The intersection and union of the set of even numbers with other sets (prime numbers, odd numbers, etc.) provide opportunities to explore different mathematical relationships and properties.
Conclusion
The seemingly mundane set of positive even numbers less than 10 — {2, 4, 6, 8} — serves as a springboard for exploring a wide array of mathematical concepts, from elementary arithmetic to advanced number theory and computer science algorithms. Its simplicity masks a deeper significance, highlighting the importance of even numbers in various fields and showcasing the interconnectedness of mathematical ideas. By understanding this small set, we gain a richer appreciation for the foundational principles that underpin more complex mathematical structures and their real-world applications. The seemingly trivial can often hold surprisingly profound insights.
Latest Posts
Latest Posts
-
4 5 As A Whole Number
May 08, 2025
-
Corresponding Sides Of Similar Triangles Are Proportional
May 08, 2025
-
3 2 7 As An Improper Fraction
May 08, 2025
-
Classifying Triangles By Angles And Sides Worksheet Pdf
May 08, 2025
-
What Are The Common Factors Of 56
May 08, 2025
Related Post
Thank you for visiting our website which covers about All Positive Even Numbers Less Than 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.