All Rational Numbers Are Natural Numbers
News Co
Apr 03, 2025 · 5 min read
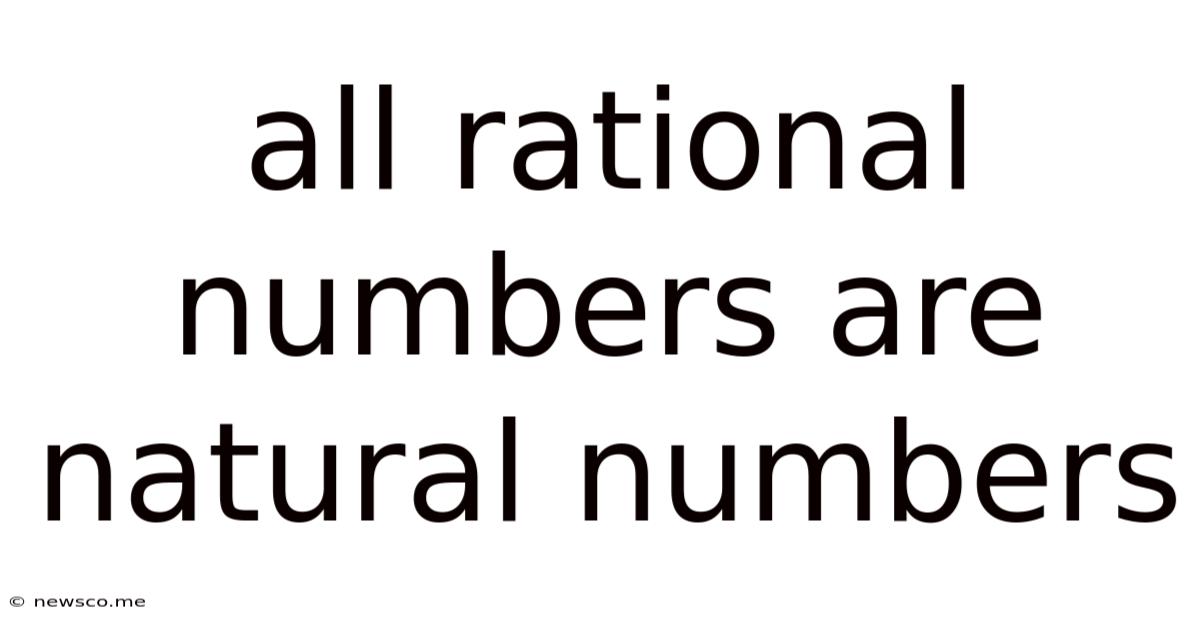
Table of Contents
All Rational Numbers are Natural Numbers: A Falsehood and its Exploration
The statement "All rational numbers are natural numbers" is false. This article will not only demonstrate the falsity of this assertion but will also delve into the definitions of rational and natural numbers, explore their relationships, and illustrate why the inclusion is incorrect through examples and counterexamples. We will also touch upon related mathematical concepts and subtly introduce essential SEO keywords throughout the text to improve search engine optimization.
Understanding Natural Numbers
Natural numbers, often denoted by the symbol ℕ, are the positive integers starting from 1 and extending infinitely. They are the numbers we use for counting: 1, 2, 3, 4, 5, and so on. This set forms the foundation of many mathematical concepts. They are also sometimes referred to as counting numbers. The inclusion or exclusion of zero (0) in the set of natural numbers varies depending on the mathematical context; some definitions include 0, while others do not. For the purpose of this article, we will consider the set ℕ to exclude zero.
Key characteristics of natural numbers:
- Positive: All natural numbers are greater than zero.
- Integers: Natural numbers are a subset of integers.
- Discrete: They are distinct, separate values; there are no natural numbers between 2 and 3, for example.
- Countable: The set of natural numbers is countable, meaning its elements can be put into a one-to-one correspondence with the natural numbers themselves.
Understanding Rational Numbers
Rational numbers, denoted by ℚ, are numbers that can be expressed as the quotient or fraction p/q of two integers, where p (the numerator) and q (the denominator) are integers, and q is not zero. This definition is crucial to understanding the relationship between rational and natural numbers. Examples of rational numbers include:
- 1/2
- 3/4
- -2/5
- 7
- 0
Key characteristics of rational numbers:
- Fractional Representation: The defining characteristic is their ability to be represented as a fraction.
- Includes Integers: All integers are rational numbers (because any integer can be written as itself divided by 1).
- Includes Decimals: Rational numbers can be represented as terminating or repeating decimals. For example, 1/2 = 0.5 (terminating), and 1/3 = 0.333... (repeating).
- Dense: Rational numbers are dense on the number line; between any two rational numbers, there exists another rational number.
Why the Statement is False: Counterexamples and Proof
The statement that all rational numbers are natural numbers is demonstrably false because rational numbers encompass a much broader range of values than natural numbers. The inclusion is simply not true. Here's why:
-
Negative Rational Numbers: Rational numbers can be negative (e.g., -1/2, -3, -22/7). Natural numbers, by definition, are always positive. This immediately invalidates the statement.
-
Fractional Rational Numbers: Many rational numbers are fractions (e.g., 1/2, 3/4, 5/8). These fractions are not whole numbers and therefore are not natural numbers.
-
Zero: While the inclusion of zero in the natural numbers is debated, it is often excluded. Zero is a rational number (0/1), but it is not a natural number (in most definitions).
Formal Proof by Counterexample:
To rigorously disprove the statement, we only need one counterexample. Let's consider the rational number -1/2. This number is clearly rational, as it can be expressed as the quotient of two integers (-1 and 2). However, -1/2 is not a natural number because natural numbers are positive integers. Therefore, the statement "All rational numbers are natural numbers" is false.
The Relationship Between Rational and Natural Numbers
While not all rational numbers are natural numbers, there is a crucial relationship: natural numbers are a subset of rational numbers. This means all natural numbers are also rational numbers. We can express any natural number as a fraction with a denominator of 1. For example:
- 5 can be written as 5/1
- 12 can be written as 12/1
- 1000 can be written as 1000/1
This illustrates the inclusion of natural numbers within the set of rational numbers. The relationship can be expressed using set notation: ℕ ⊂ ℚ (ℕ is a proper subset of ℚ).
Expanding on Irrational Numbers
To further clarify the differences, it's useful to introduce irrational numbers. Irrational numbers are numbers that cannot be expressed as a fraction of two integers. Examples include π (pi), √2 (the square root of 2), and e (Euler's number). Irrational numbers have non-repeating, non-terminating decimal expansions. This contrasts with rational numbers, which have either terminating or repeating decimals.
The combination of rational and irrational numbers makes up the set of real numbers (denoted by ℝ). The real numbers encompass all the numbers on the number line. The relationship can be visualized using a Venn diagram, showing the natural numbers as a subset of rational numbers, which in turn is a subset of real numbers. Irrational numbers are also a subset of real numbers, but they do not intersect with the set of rational numbers.
Implications and Further Exploration
Understanding the distinction between rational and natural numbers is fundamental in various areas of mathematics, including:
- Number Theory: The study of integers and their properties heavily relies on the properties of rational and natural numbers.
- Algebra: Rational numbers are essential in solving equations and inequalities.
- Calculus: Rational and irrational numbers play a vital role in the study of limits, derivatives, and integrals.
- Analysis: The concepts of convergence and continuity in analysis are closely tied to the properties of rational and irrational numbers.
- Computer Science: Representing and manipulating numbers in computer systems often involves working with rational numbers and their approximations.
Further exploration could involve delving into different number systems, such as complex numbers, ordinal numbers, and cardinal numbers. Each of these systems has its own unique properties and expands our understanding of the vast landscape of mathematical concepts.
Conclusion: A Clear Distinction
The statement "All rational numbers are natural numbers" is incorrect. While natural numbers are a subset of rational numbers, the converse is not true. Rational numbers include a much wider range of values, encompassing negative numbers, fractions, and zero. This fundamental difference underscores the importance of precisely defining mathematical terms and understanding the relationships between different number sets. This article has provided a comprehensive explanation using examples, counterexamples, and a formal approach to highlight the error and solidify the understanding of these critical mathematical concepts. We hope this exploration has enhanced your understanding of number systems and their importance in mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about All Rational Numbers Are Natural Numbers . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.