An Irrational Number With A Value Greater Than 10
News Co
May 07, 2025 · 5 min read
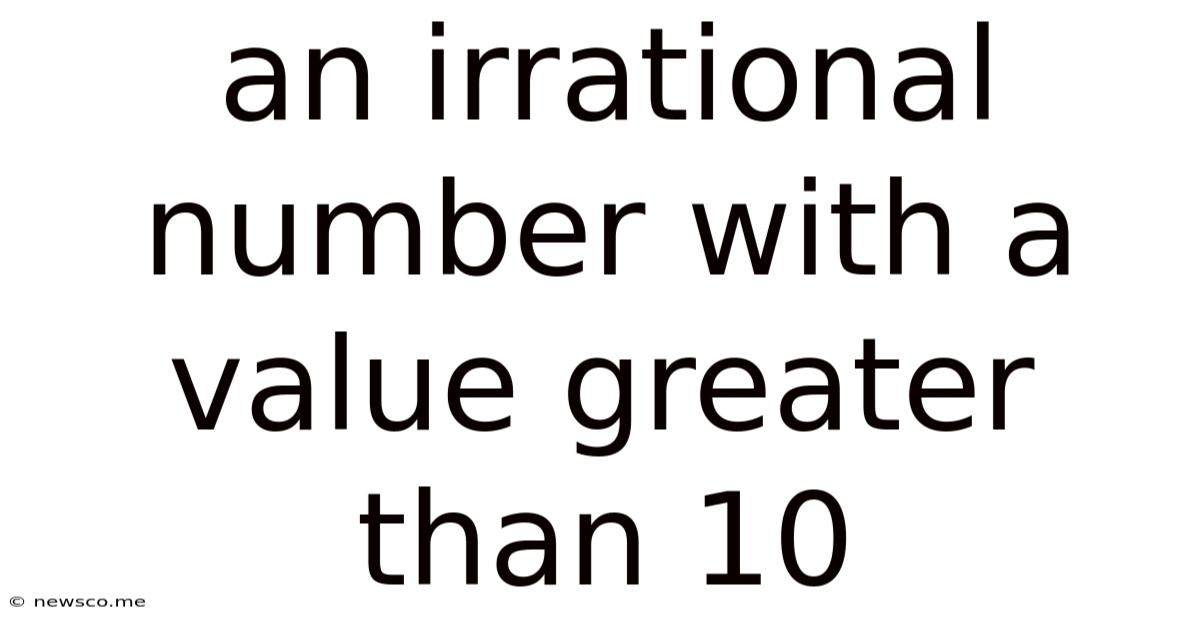
Table of Contents
An Irrational Number Greater Than 10: Exploring the Infinite
The world of numbers is vast and captivating, filled with both the familiar and the utterly mysterious. While we readily interact with rational numbers—those expressible as a simple fraction—a whole other realm exists: the realm of irrational numbers. These numbers, by definition, cannot be expressed as a fraction of two integers. Their decimal representations neither terminate nor repeat, stretching infinitely without discernible pattern. This article delves into the fascinating world of irrational numbers, focusing specifically on those exceeding the value of 10. We’ll explore how such numbers are generated, their significance in mathematics, and the inherent mysteries they hold.
Understanding Irrational Numbers
Before venturing into the realm of irrational numbers greater than 10, let's solidify our understanding of what constitutes an irrational number. The core characteristic is their inability to be expressed as a ratio (fraction) of two integers. This means their decimal expansions are non-terminating and non-repeating. Examples include:
-
π (Pi): Approximately 3.14159..., representing the ratio of a circle's circumference to its diameter. Its infinite and non-repeating decimal expansion has captivated mathematicians for centuries.
-
e (Euler's number): Approximately 2.71828..., the base of the natural logarithm. Like π, its decimal representation continues indefinitely without repetition.
-
√2 (the square root of 2): Approximately 1.41421..., representing the length of the diagonal of a square with sides of length 1. This was one of the first numbers proven to be irrational.
These are just a few of the well-known irrational numbers. However, the vast majority of irrational numbers are far less familiar, often arising from more complex mathematical operations or constructions.
Constructing Irrational Numbers Greater Than 10
Creating irrational numbers greater than 10 involves leveraging the properties of known irrational numbers or employing mathematical operations that inherently generate irrational results. Here are a few methods:
1. Sums and Products
A simple method involves adding or multiplying known irrational numbers. For instance:
-
10 + π: This directly produces an irrational number greater than 10. Since π is irrational, adding it to any rational number (like 10) will result in an irrational number. The resulting number is approximately 13.14159...
-
10 * √2: Similarly, multiplying a rational number (10) by an irrational number (√2) yields an irrational result. This results in a number approximately equal to 14.1421...
-
π * e: The product of two well-known irrational numbers also yields an irrational number greater than 10 (approximately 8.53973...). While this result is not directly greater than 10, we can easily modify this by adding a sufficient rational number to surpass 10.
These examples demonstrate that simple arithmetic operations involving at least one irrational number can easily produce irrational numbers exceeding 10.
2. Nested Radicals
Nested radicals, where square roots (or other roots) are embedded within each other, are a rich source of irrational numbers. Consider the following:
√(100 + √(100 + √(100 + ...)))
This expression, if it converges, will produce an irrational number greater than 10. The iterative nature of the expression guarantees a non-repeating, non-terminating decimal expansion. While determining its precise value might be computationally intensive, its irrationality is inherent in its construction.
3. Transcendental Numbers
Transcendental numbers are a special subset of irrational numbers. They are numbers that are not the roots of any non-zero polynomial with rational coefficients. Many transcendental numbers are significantly larger than 10. While explicitly constructing them might require advanced mathematical tools, their existence proves the abundance of large irrational numbers. Examples include specific values of the exponential function or trigonometric functions evaluated at transcendental inputs.
The Significance of Irrational Numbers Greater Than 10
While the immediate practical applications of an arbitrary irrational number greater than 10 might seem limited compared to, say, π, their existence holds deep mathematical significance:
-
Illustrating the Density of Irrational Numbers: The fact that we can easily construct irrational numbers greater than 10 illustrates the sheer density of irrational numbers within the real number system. Between any two rational numbers, there exist infinitely many irrational numbers.
-
Expanding Mathematical Concepts: The study of irrational numbers helps to expand our understanding of fundamental mathematical concepts, like limits, continuity, and infinity.
-
Foundation for Advanced Mathematics: Irrational numbers are essential building blocks for advanced mathematical concepts and theories, including calculus, analysis, and number theory.
The Mysteries of Irrational Numbers
Despite centuries of study, the world of irrational numbers continues to hold many mysteries. Some open questions and areas of ongoing research include:
-
Normal Numbers: A normal number is one whose digits are equally distributed in all bases. While it's suspected that many irrational numbers are normal, proving normality remains a significant challenge. Many large irrational numbers might fit into this category, awaiting investigation.
-
Computational Challenges: Calculating the precise value of complex irrational numbers is often computationally challenging, requiring advanced algorithms and substantial computing power. Many large irrational numbers present significant computational hurdles.
-
Understanding the Distribution of Digits: The seemingly random distribution of digits in the decimal expansions of many irrational numbers continues to intrigue mathematicians. Predicting the distribution of digits in large irrational numbers is a complex problem.
Conclusion: A Universe of Unknowns
The existence of irrational numbers greater than 10, while not immediately intuitive, serves as a compelling reminder of the vastness and complexity of the mathematical universe. These numbers, born from simple operations or intricate mathematical constructs, highlight the infinite nature of the real number line and the ongoing challenges and mysteries that surround them. Their study expands our understanding of fundamental mathematical principles, driving further research and uncovering deeper truths about the nature of numbers themselves. The seemingly simple concept of a number greater than 10 expands into a rich tapestry of infinite possibilities when considering irrational numbers, leaving us with a sense of awe and wonder at the mysteries that still remain to be unlocked.
Latest Posts
Related Post
Thank you for visiting our website which covers about An Irrational Number With A Value Greater Than 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.