Angles Formed By A Transversal Worksheet
News Co
Apr 06, 2025 · 5 min read
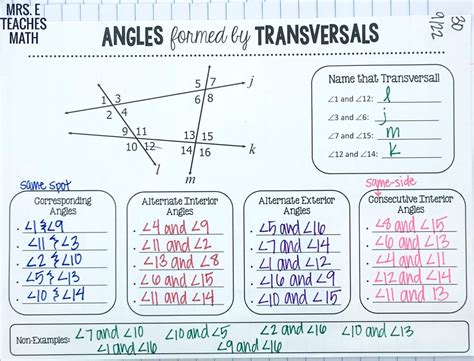
Table of Contents
Angles Formed by a Transversal Worksheet: A Comprehensive Guide
Understanding angles formed by a transversal is crucial for mastering geometry. This comprehensive guide will delve into the intricacies of transversal lines, exploring the various angle relationships they create and providing you with ample practice through worksheets and examples. We will cover parallel lines, perpendicular lines, and the different types of angles, ensuring you gain a solid grasp of this fundamental geometric concept.
What is a Transversal Line?
A transversal line is a line that intersects two or more other lines at distinct points. These intersected lines can be parallel, perpendicular, or neither. The transversal's intersection creates various angles, and understanding the relationships between these angles is key to solving geometric problems.
Types of Angles Formed by a Transversal
When a transversal intersects two lines, eight angles are formed. These angles can be categorized into several types based on their relationships:
-
Corresponding Angles: These angles are located in the same relative position at the intersection of the transversal and the two lines. They are equal if the intersected lines are parallel.
-
Alternate Interior Angles: These angles are located between the two lines and on opposite sides of the transversal. They are also equal if the intersected lines are parallel.
-
Alternate Exterior Angles: These angles are located outside the two lines and on opposite sides of the transversal. Similar to alternate interior angles, they are equal if the lines are parallel.
-
Consecutive Interior Angles (Same-Side Interior Angles): These angles are located between the two lines and on the same side of the transversal. They are supplementary (add up to 180°) if the intersected lines are parallel.
-
Consecutive Exterior Angles (Same-Side Exterior Angles): These angles are located outside the two lines and on the same side of the transversal. They are also supplementary (add up to 180°) if the intersected lines are parallel.
-
Vertical Angles: These angles are formed by intersecting lines and are opposite each other. They are always equal. This relationship holds true regardless of whether the intersected lines are parallel.
Parallel Lines and Transversals: The Key Relationships
When a transversal intersects two parallel lines, specific relationships exist between the angles formed:
-
Corresponding Angles are Congruent: This means they have the same measure.
-
Alternate Interior Angles are Congruent: These angles are equal in measure.
-
Alternate Exterior Angles are Congruent: These angles are also equal in measure.
-
Consecutive Interior Angles are Supplementary: Their sum is 180°.
-
Consecutive Exterior Angles are Supplementary: Their sum is also 180°.
This understanding of congruent and supplementary angles is fundamental to solving problems involving parallel lines and transversals.
Worksheet 1: Identifying Angle Relationships
This worksheet will focus on identifying the different types of angles formed by a transversal intersecting two lines. Remember to consider whether the lines are parallel to determine the angle relationships.
(Diagram showing two parallel lines intersected by a transversal would be included here. The diagram should clearly label angles 1 through 8.)
Instructions: Identify the relationship between the following pairs of angles (e.g., corresponding, alternate interior, etc.):
- ∠1 and ∠5
- ∠2 and ∠6
- ∠3 and ∠7
- ∠4 and ∠8
- ∠1 and ∠8
- ∠2 and ∠7
- ∠3 and ∠6
- ∠4 and ∠5
Worksheet 2: Solving for Unknown Angles
This worksheet will challenge you to use the angle relationships to find the measures of unknown angles. Assume the lines are parallel unless otherwise stated.
(Diagram showing two parallel lines intersected by a transversal with some angles labeled with their measures and others labeled with variables like x, y, z would be included here.)
Instructions: Find the measure of each unknown angle:
- If ∠1 = 70°, find ∠5, ∠6, ∠7, and ∠8.
- If ∠2 = 110°, find ∠4, ∠5, ∠6, and ∠7.
- If ∠3 = 65°, find ∠1, ∠2, ∠5, and ∠8.
- If ∠4 = 115°, find ∠1, ∠2, ∠6, and ∠7.
- If ∠1 and ∠3 are vertical angles and ∠1 = 45°, find the measure of all other angles.
Worksheet 3: Proofs and Applications
This worksheet involves more complex problems that require applying the angle relationships in proofs and real-world scenarios.
(Diagrams showing various situations with parallel lines and transversals, including some non-parallel lines, would be included here.)
Instructions:
-
Proof: Prove that if two parallel lines are cut by a transversal, then consecutive interior angles are supplementary. Write a two-column geometric proof.
-
Problem Solving: A carpenter is building a staircase. The handrail is parallel to the stringers. The support posts form a transversal. If the angle between a support post and a stringer is 130°, what is the measure of the angle between the support post and the handrail? Draw a diagram to illustrate the problem.
-
Critical Thinking: Two lines are intersected by a transversal. If one pair of alternate interior angles is congruent, what can you conclude about the two lines? Explain your reasoning.
-
Advanced Problem: Three parallel lines are intersected by two transversals. Explain how you would determine the measures of all the angles formed.
Perpendicular Lines and Transversals
When a transversal intersects two perpendicular lines, all the angles formed are right angles (90°). This simplifies the relationships significantly. Every angle will measure 90°.
Non-Parallel Lines and Transversals
When a transversal intersects two non-parallel lines, the angle relationships discussed for parallel lines do not apply. The angles formed will have various measures, and there are no specific relationships between them except for vertical angles which remain always equal. Solving problems involving non-parallel lines often requires using other geometric principles and information provided in the problem.
Troubleshooting Common Mistakes
-
Incorrect Angle Identification: Carefully label and identify each angle before attempting to solve problems. Use consistent notation.
-
Confusing Angle Relationships: Review the definitions of corresponding angles, alternate interior angles, alternate exterior angles, and consecutive interior/exterior angles. Understand the conditions under which these relationships hold true (parallel lines).
-
Ignoring Vertical Angles: Remember that vertical angles are always congruent. Use this fact to your advantage in solving problems.
-
Not Drawing Diagrams: Always draw a diagram to visualize the problem. This helps you identify the angles and their relationships.
By diligently working through these worksheets and understanding the fundamental concepts explained, you'll develop a strong foundation in understanding angles formed by a transversal. This knowledge is essential for success in further geometry studies and various applications in other fields. Remember to practice regularly and consult additional resources if needed. Mastering these concepts will significantly enhance your problem-solving skills and geometric intuition.
Latest Posts
Related Post
Thank you for visiting our website which covers about Angles Formed By A Transversal Worksheet . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.