Are 3/4 And 9/12 Equivalent Fractions
News Co
Mar 29, 2025 · 5 min read
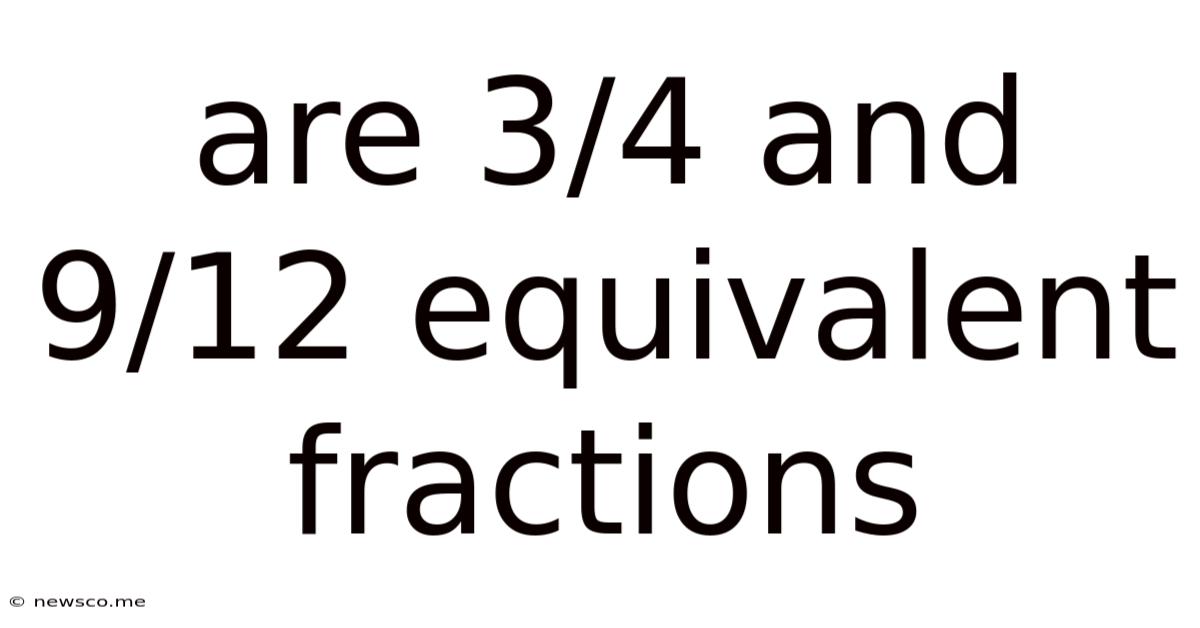
Table of Contents
Are 3/4 and 9/12 Equivalent Fractions? A Deep Dive into Fraction Equivalence
Understanding equivalent fractions is a cornerstone of mathematical literacy. It's a concept that extends far beyond simple arithmetic, influencing our ability to solve complex problems in algebra, geometry, and even calculus. This article will delve into the question, "Are 3/4 and 9/12 equivalent fractions?", exploring not just the answer but the underlying principles and practical applications of fraction equivalence. We'll equip you with the knowledge and tools to confidently determine the equivalence of any two fractions.
What are Equivalent Fractions?
Equivalent fractions represent the same portion or value, even though they look different. Imagine cutting a pizza: One half (1/2) is the same amount as two quarters (2/4), or four eighths (4/8), even though the number of slices varies. These different representations are all equivalent fractions because they all denote the same portion of the whole pizza.
The key to understanding equivalent fractions lies in the concept of simplification or reducing fractions to their lowest terms. This process involves dividing both the numerator (the top number) and the denominator (the bottom number) by their greatest common divisor (GCD), also known as the greatest common factor (GCF). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
Finding the Greatest Common Divisor (GCD)
Several methods can be used to find the GCD of two numbers. Let's explore a few:
1. Listing Factors:
This method involves listing all the factors of both the numerator and the denominator and then identifying the largest factor they share. For example, let's find the GCD of 12 and 18:
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
The greatest common factor is 6.
2. Prime Factorization:
This method involves breaking down both numbers into their prime factors (numbers only divisible by 1 and themselves). Then, we identify the common prime factors and multiply them together to find the GCD. Let's use the same example of 12 and 18:
- Prime factorization of 12: 2 x 2 x 3
- Prime factorization of 18: 2 x 3 x 3
The common prime factors are 2 and 3. Multiplying them gives us 2 x 3 = 6, which is the GCD.
3. Euclidean Algorithm:
This is a more efficient method for larger numbers. It involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD. Let's illustrate with 12 and 18:
- 18 ÷ 12 = 1 with a remainder of 6
- 12 ÷ 6 = 2 with a remainder of 0
The last non-zero remainder is 6, so the GCD is 6.
Determining Equivalence: The Case of 3/4 and 9/12
Now, let's address the core question: Are 3/4 and 9/12 equivalent fractions?
To determine this, we can use several approaches:
1. Simplifying 9/12:
Let's find the GCD of 9 and 12 using any of the methods above. The GCD is 3. Dividing both the numerator and denominator of 9/12 by 3, we get:
9 ÷ 3 / 12 ÷ 3 = 3/4
Since simplifying 9/12 results in 3/4, yes, 3/4 and 9/12 are equivalent fractions.
2. Cross-Multiplication:
Another way to check for equivalence is through cross-multiplication. If the product of the numerator of one fraction and the denominator of the other fraction equals the product of the denominator of the first fraction and the numerator of the second fraction, then the fractions are equivalent.
For 3/4 and 9/12:
- 3 x 12 = 36
- 4 x 9 = 36
Since both products are equal, 3/4 and 9/12 are equivalent fractions.
3. Visual Representation:
Imagine a rectangle divided into four equal parts. Shading three parts represents 3/4. Now, imagine the same rectangle divided into twelve equal parts. Shading nine parts represents 9/12. Visually, you'll see that both representations cover the same area, confirming their equivalence.
Practical Applications of Equivalent Fractions
Understanding equivalent fractions is crucial in various mathematical and real-world contexts:
-
Simplifying Calculations: Working with smaller numbers (after simplifying a fraction) makes calculations easier and less prone to errors.
-
Comparing Fractions: Finding equivalent fractions with a common denominator facilitates the comparison of fractions with different denominators. For example, comparing 2/3 and 3/4 is easier after converting them to 8/12 and 9/12, respectively.
-
Solving Equations: In algebra, equivalent fractions are essential for solving equations involving fractions.
-
Measurement and Conversions: Equivalent fractions are vital in converting units of measurement (e.g., inches to feet, centimeters to meters).
-
Ratio and Proportion: Equivalent fractions form the basis of ratios and proportions, which are widely used in various fields such as cooking, construction, and engineering.
Beyond the Basics: Exploring More Complex Scenarios
The principles we've discussed apply to all fractions, including those with larger numbers or mixed numbers (a whole number and a fraction).
Example with larger numbers: Are 24/36 and 18/27 equivalent? Simplifying both fractions reveals that they both reduce to 2/3.
Example with mixed numbers: Are 1 1/2 and 3/2 equivalent? Converting the mixed number 1 1/2 to an improper fraction (3/2) demonstrates their equivalence.
Conclusion: Mastering Fraction Equivalence
The ability to identify equivalent fractions is a fundamental skill in mathematics. By understanding the concept of GCD, simplification, and different methods for checking equivalence, you can confidently work with fractions in various contexts. The question, "Are 3/4 and 9/12 equivalent fractions?" serves as a stepping stone to a deeper understanding of this critical mathematical concept, which will serve you well throughout your mathematical journey. Remember to practice regularly to solidify your understanding and build confidence in working with fractions. Through consistent practice and application, you will master this essential skill. The more you engage with fractions and their properties, the more natural and intuitive the concept of equivalence will become. Don't hesitate to explore additional resources and practice problems to further enhance your understanding.
Latest Posts
Related Post
Thank you for visiting our website which covers about Are 3/4 And 9/12 Equivalent Fractions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.