C 5 9 F 32 Solve For F
News Co
Apr 12, 2025 · 5 min read
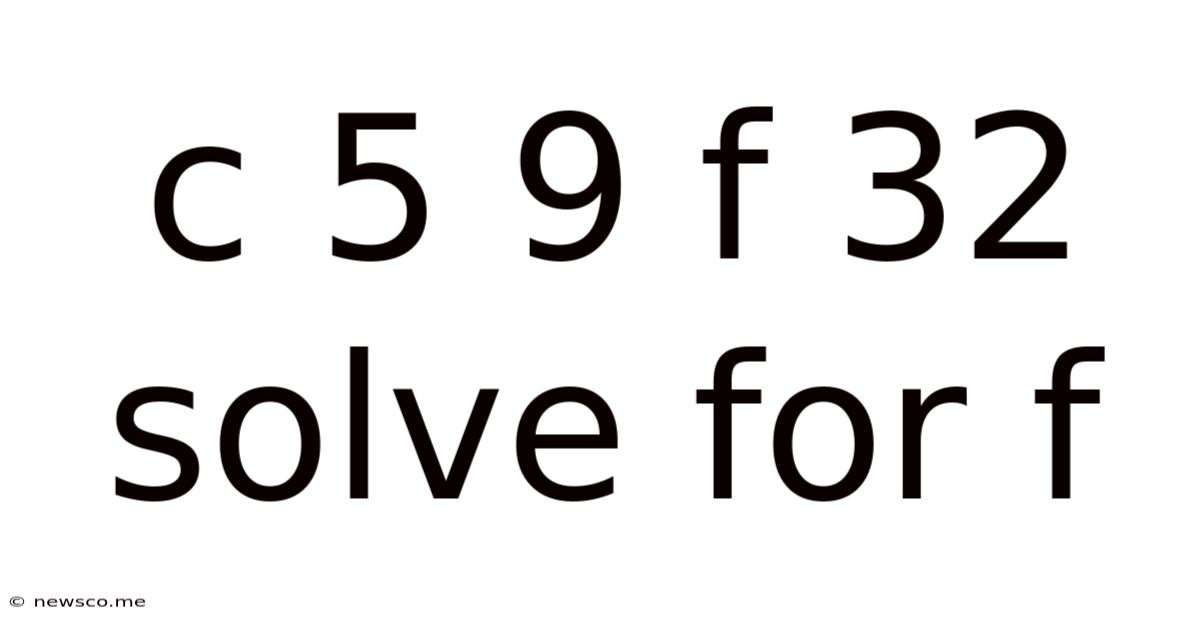
Table of Contents
Solving for F: A Comprehensive Guide to the Celsius-Fahrenheit Conversion
The equation C/5 = (F-32)/9 is a fundamental formula in physics and everyday life, used to convert temperatures between the Celsius (°C) and Fahrenheit (°F) scales. While seemingly simple, understanding how to manipulate this equation to solve for any of its variables—particularly 'F'—is crucial for anyone working with temperature conversions. This article will provide a comprehensive guide on solving for F, explaining the process step-by-step, exploring different methods, and offering practical examples. We’ll also delve into the underlying principles of the conversion, ensuring a thorough understanding of the formula’s significance.
Understanding the Celsius-Fahrenheit Conversion Formula
Before diving into solving for F, let's briefly examine the equation itself: C/5 = (F-32)/9. This formula demonstrates the proportional relationship between Celsius and Fahrenheit. It states that the difference between a temperature in Fahrenheit and 32 degrees is nine-ninths the difference between the corresponding temperature in Celsius and zero degrees.
Why is 32 crucial?
The number 32 holds significant meaning. 0°C corresponds to 32°F, the freezing point of water. This offset of 32 degrees reflects a fundamental difference in how the scales were originally defined.
The Significance of 5 and 9
The ratio 5/9 (or its reciprocal, 9/5) reflects the differing magnitudes of a degree in each scale. A change of 1°C is equal to a change of 9/5°F, illustrating that a Fahrenheit degree is smaller than a Celsius degree.
Solving for F: A Step-by-Step Approach
To solve for F, we need to isolate the variable 'F' on one side of the equation. This involves applying algebraic manipulation techniques, focusing on reversing the operations performed on 'F'.
Step 1: Eliminate the Fraction
Begin by eliminating the fraction containing 'F'. We can achieve this by multiplying both sides of the equation by 9:
9 * (C/5) = 9 * ((F-32)/9)
This simplifies to:
(9C)/5 = F - 32
Step 2: Isolate F
Next, isolate 'F' by adding 32 to both sides of the equation:
(9C)/5 + 32 = F - 32 + 32
This simplifies to:
F = (9C)/5 + 32
This is our final formula for converting Celsius to Fahrenheit.
Alternative Methods for Solving for F
While the step-by-step method is the most straightforward, understanding alternative approaches can enhance your problem-solving skills. Let's explore another common method.
Using Cross-Multiplication
Cross-multiplication offers an alternative approach to solving for 'F':
C/5 = (F-32)/9
Cross-multiplying gives:
9C = 5(F-32)
Distribute the 5:
9C = 5F - 160
Add 160 to both sides:
9C + 160 = 5F
Divide both sides by 5:
F = (9C + 160)/5
This formula is mathematically equivalent to the one derived using the step-by-step method, demonstrating the flexibility of algebraic manipulation.
Practical Applications and Examples
Let's solidify our understanding with some practical examples:
Example 1: Converting 20°C to Fahrenheit
Using the formula F = (9C)/5 + 32:
F = (9 * 20)/5 + 32 = 36 + 32 = 68°F
Example 2: Converting 0°C to Fahrenheit
Using the formula F = (9C)/5 + 32:
F = (9 * 0)/5 + 32 = 0 + 32 = 32°F (This confirms the freezing point of water)
Example 3: Converting 100°C to Fahrenheit
Using the formula F = (9C)/5 + 32:
F = (9 * 100)/5 + 32 = 180 + 32 = 212°F (This confirms the boiling point of water)
Example 4: Solving for F using the alternative formula:
Let's use the alternative formula F = (9C + 160)/5 and convert 25°C to Fahrenheit:
F = (9 * 25 + 160)/5 = (225 + 160)/5 = 385/5 = 77°F
Beyond the Formula: Understanding the Scales
The Celsius and Fahrenheit scales, while both measuring temperature, differ significantly in their construction. Understanding these differences adds depth to the conversion process.
Celsius (Centigrade) Scale
The Celsius scale, also known as the centigrade scale, is based on the freezing and boiling points of water. 0°C represents the freezing point, and 100°C represents the boiling point at standard atmospheric pressure. This creates a 100-degree interval between these two key points.
Fahrenheit Scale
The Fahrenheit scale is based on a different set of reference points and has a larger degree interval. Its origins lie in Daniel Gabriel Fahrenheit's early temperature measurements. 32°F represents the freezing point of water, and 212°F represents the boiling point at standard atmospheric pressure.
Troubleshooting and Common Mistakes
While the conversion process itself is relatively straightforward, certain mistakes commonly occur. Let's address some frequent challenges:
- Order of Operations: Always follow the order of operations (PEMDAS/BODMAS). Parentheses, exponents, multiplication and division (from left to right), then addition and subtraction (from left to right). Failing to do so can lead to incorrect results.
- Incorrect Formula: Ensure you use the correct formula, either F = (9C)/5 + 32 or its equivalent. Using a different or altered formula will inevitably produce wrong results.
- Calculation Errors: Double-check your calculations. Simple arithmetic errors can easily lead to incorrect conversions. Use a calculator if necessary and verify your work.
Advanced Applications and Extensions
The Celsius-Fahrenheit conversion is a foundational concept applicable to various fields, extending beyond simple temperature conversions:
- Meteorology: Weather reports often utilize both scales, and conversions are essential for interpreting data from different sources.
- Engineering: Various engineering disciplines, including thermodynamics and material science, rely on temperature conversions for accurate calculations and analysis.
- Cooking and Baking: Precise temperature control is crucial in culinary arts, demanding accurate conversions between Celsius and Fahrenheit when following recipes from different regions.
- Scientific Research: Numerous scientific experiments involve temperature measurements, and the ability to convert between scales is paramount for data consistency and interpretation.
Conclusion
Solving for F in the equation C/5 = (F-32)/9 is a fundamental skill with broad applications. Mastering this conversion, understanding the underlying principles of the Celsius and Fahrenheit scales, and practicing with various examples will enhance your problem-solving abilities and broaden your understanding of temperature measurements. Remember to always double-check your work, and don't hesitate to utilize a calculator for complex calculations. The seemingly simple equation C/5 = (F-32)/9 opens doors to a deeper understanding of the world around us, highlighting the interconnectedness of seemingly disparate fields through the common language of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about C 5 9 F 32 Solve For F . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.