C 5 9 F 32 Solve For F Answer
News Co
Apr 26, 2025 · 4 min read
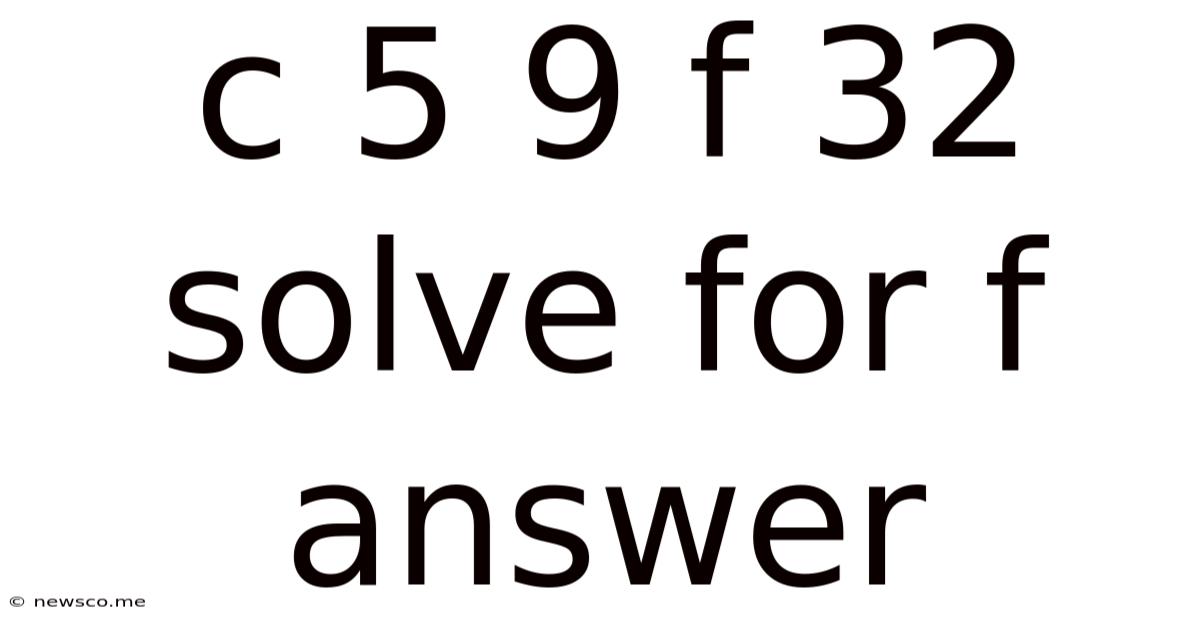
Table of Contents
Solving for F: A Deep Dive into the Celsius to Fahrenheit Conversion Formula
The simple equation, C = 5/9(F - 32), represents the conversion between Celsius (°C) and Fahrenheit (°F), two widely used temperature scales. Understanding how to manipulate this formula to solve for F is crucial in numerous scientific, engineering, and everyday applications. This comprehensive guide will not only show you how to solve for F but also delve into the underlying principles, provide practical examples, and offer tips for mastering algebraic manipulations.
Understanding the Celsius to Fahrenheit Conversion Formula
Before jumping into the solution, let's break down the equation: C = 5/9(F - 32).
- C: Represents the temperature in degrees Celsius.
- F: Represents the temperature in degrees Fahrenheit.
- 5/9: This fraction is the conversion factor between the scales. It reflects the difference in the size of one degree Celsius compared to one degree Fahrenheit.
- (F - 32): This part accounts for the difference in the zero points of the two scales. Water freezes at 0°C and 32°F, highlighting this offset.
The formula essentially states that a Celsius temperature is obtained by taking the Fahrenheit temperature, subtracting 32, and then multiplying the result by 5/9.
Solving for F: Step-by-Step Process
Our goal is to isolate F on one side of the equation. Here's how we do it, explained step-by-step:
1. Eliminate the Fraction:
The first step is to eliminate the fraction 5/9. We can do this by multiplying both sides of the equation by 9:
9C = 9 * (5/9)(F - 32)
This simplifies to:
9C = 5(F - 32)
2. Distribute the 5:
Next, we distribute the 5 to the terms inside the parenthesis:
9C = 5F - 160
3. Isolate the Term with F:
Now, we want to isolate the term containing F. To do this, we add 160 to both sides of the equation:
9C + 160 = 5F
4. Solve for F:
Finally, to completely isolate F, we divide both sides of the equation by 5:
(9C + 160) / 5 = F
Therefore, the solution for F is:
F = (9C + 160) / 5
This is the formula to convert Celsius to Fahrenheit.
Practical Examples: Putting the Formula to Work
Let's solidify our understanding with some practical examples:
Example 1: Converting 20°C to Fahrenheit
Substitute C = 20 into the formula:
F = (9 * 20 + 160) / 5 = (180 + 160) / 5 = 340 / 5 = 68°F
Therefore, 20°C is equal to 68°F.
Example 2: Converting 0°C to Fahrenheit
Substitute C = 0 into the formula:
F = (9 * 0 + 160) / 5 = 160 / 5 = 32°F
This confirms the freezing point of water: 0°C = 32°F.
Example 3: Converting -40°C to Fahrenheit
Substitute C = -40 into the formula:
F = (9 * -40 + 160) / 5 = (-360 + 160) / 5 = -200 / 5 = -40°F
This is a unique point where both Celsius and Fahrenheit scales coincide: -40°C = -40°F.
Beyond the Basics: Advanced Applications and Considerations
The ability to solve for F opens doors to more complex applications:
- Programming: This formula is frequently used in programming to convert temperature units within applications.
- Data Analysis: Scientists and engineers often need to convert temperature data between Celsius and Fahrenheit for analysis and reporting.
- Weather Forecasting: Understanding the conversion is vital for interpreting weather information from different sources.
- Engineering Design: Precise temperature conversions are crucial in engineering designs involving thermal systems and materials.
Error Handling and Data Validation
When working with real-world data, consider implementing error handling:
- Input Validation: Check if the input value for C is a valid number.
- Range Checks: Ensure the input is within a reasonable range for temperature measurements.
- Output Validation: Verify the calculated F value is within realistic temperature bounds.
Alternative Approaches and Approximations
While the precise formula is ideal, approximations can be useful in certain contexts:
- Rule of Thumb: A quick approximation is to double the Celsius temperature and add 30. This method works reasonably well for temperatures around room temperature but becomes less accurate at extreme temperatures.
Mastering Algebraic Manipulation: Tips and Techniques
Solving for F requires a strong grasp of algebraic manipulation. Here are some key techniques:
- Order of Operations (PEMDAS/BODMAS): Always follow the order of operations to ensure accurate calculations.
- Inverse Operations: Use inverse operations (addition/subtraction, multiplication/division) to isolate the variable.
- Distributive Property: Understanding the distributive property is key to expanding expressions.
- Practice: Consistent practice is crucial to mastering algebraic manipulations.
Conclusion: From Equation to Understanding
Solving for F in the Celsius to Fahrenheit conversion formula is more than just an algebraic exercise. It's a gateway to understanding fundamental concepts in temperature measurement and a crucial skill applicable across various fields. By mastering this simple yet powerful equation, you've equipped yourself with a valuable tool for problem-solving and data analysis. Remember to practice regularly and explore the advanced applications to further enhance your understanding. This comprehensive guide has provided you with the knowledge and tools necessary to confidently handle Celsius to Fahrenheit conversions.
Latest Posts
Related Post
Thank you for visiting our website which covers about C 5 9 F 32 Solve For F Answer . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.