Can A Triangle Be Isosceles And Right
News Co
Apr 05, 2025 · 5 min read
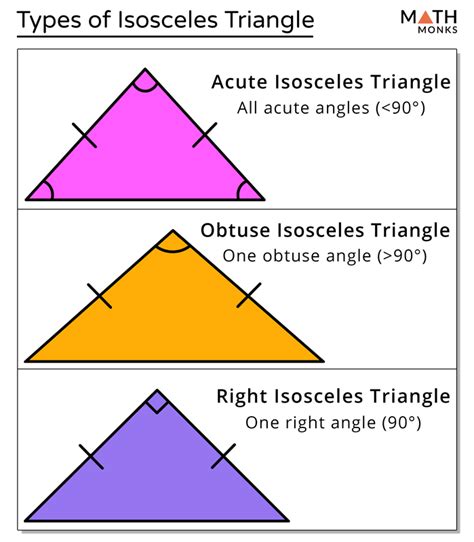
Table of Contents
Can a Triangle Be Isosceles and Right? Exploring the Geometry of Special Triangles
The question of whether a triangle can simultaneously be isosceles and right-angled is a fundamental concept in geometry. Understanding the properties of isosceles and right-angled triangles, and how these properties might intersect, requires a deeper dive into geometric principles. This article will explore this fascinating intersection, examining the definitions of both types of triangles, and rigorously proving whether or not such a triangle exists. We’ll also touch on the implications of this exploration for solving various geometric problems.
Defining Isosceles and Right-Angled Triangles
Before we investigate the possibility of a triangle being both isosceles and right-angled, let's solidify our understanding of each type individually.
Isosceles Triangles: The Definition
An isosceles triangle is defined as a triangle with at least two sides of equal length. These equal sides are called the legs, and the angle between them is called the apex angle. The third side, which is potentially of a different length, is called the base. Crucially, the definition doesn't specify exactly two equal sides; it allows for the possibility of all three sides being equal, which would also classify the triangle as equilateral (a special case of an isosceles triangle).
Key characteristics of isosceles triangles:
- Two equal sides: This is the defining characteristic.
- Two equal angles: The angles opposite the equal sides are also equal (this is a consequence of the Isosceles Triangle Theorem).
- Line of symmetry: An isosceles triangle possesses a line of symmetry that bisects the apex angle and the base.
Right-Angled Triangles: The Definition
A right-angled triangle (or right triangle) is defined as a triangle containing one angle that measures exactly 90 degrees (a right angle). This right angle is often denoted with a small square in the corner. The side opposite the right angle is called the hypotenuse, and is always the longest side in a right-angled triangle. The other two sides are called legs or cathetus.
Key characteristics of right-angled triangles:
- One 90-degree angle: This is the defining characteristic.
- Pythagorean Theorem: The relationship between the sides is governed by the Pythagorean Theorem (a² + b² = c², where a and b are the legs and c is the hypotenuse).
- Trigonometric functions: Right-angled triangles are fundamental to trigonometry, allowing us to define trigonometric ratios like sine, cosine, and tangent.
Can a Triangle Be Both Isosceles and Right-Angled? A Proof
Now, let's address the central question: Can a triangle be both isosceles and right-angled? The answer is a resounding yes. To prove this, we need to demonstrate that it is geometrically possible to construct such a triangle.
Construction and Proof:
Consider a right-angled triangle. Let's label the right angle as angle C, and the other two angles as A and B. Since the angles in any triangle add up to 180 degrees, we have:
A + B + C = 180°
Given that C = 90°, we get:
A + B + 90° = 180°
A + B = 90°
For the triangle to be isosceles, at least two of its angles must be equal. Let's assume that angles A and B are equal: A = B. Substituting this into our equation:
A + A = 90°
2A = 90°
A = 45°
Since A = B, we also have B = 45°. Therefore, we have a right-angled triangle with angles of 45°, 45°, and 90°. This is a perfectly valid triangle, fulfilling both the isosceles and right-angled criteria. The sides opposite the 45° angles will be equal in length.
Visual Representation:
Imagine a square. Draw a diagonal line across it. This diagonal line divides the square into two identical right-angled triangles. Each triangle has two equal sides (the sides of the square) and a right angle where the sides of the square meet. The angles are 45°, 45°, and 90°. This clearly demonstrates the existence of a triangle that is both isosceles and right-angled.
The 45-45-90 Triangle: Properties and Applications
The 45-45-90 triangle, also known as an isosceles right triangle, is a special type of right triangle with unique properties that make it incredibly useful in various fields:
Properties:
- Angles: 45°, 45°, 90°
- Sides: The ratio of the sides is 1:1:√2 (legs:hypotenuse). If the legs have length 'x', the hypotenuse has length x√2.
- Symmetry: It is symmetric about the altitude drawn from the right angle to the hypotenuse.
- Area: The area is given by (x²/2), where x is the length of a leg.
Applications:
The 45-45-90 triangle finds application in numerous areas, including:
- Engineering: In structural design, especially when dealing with symmetrical structures.
- Architecture: Used in calculating dimensions and angles in building designs.
- Physics: In solving problems involving vectors and forces.
- Computer graphics: Used extensively in image manipulation and 3D modeling.
- Navigation: Helps in calculating distances and directions.
Distinguishing Isosceles Right Triangles from Other Triangles
It's important to differentiate the 45-45-90 triangle from other types of triangles to avoid confusion:
- Equilateral Triangle: An equilateral triangle has three equal sides and three equal 60° angles. It's not a right-angled triangle.
- Scalene Right Triangle: A scalene right triangle has three unequal sides, with one angle being 90°.
- Isosceles Acute Triangle: An isosceles acute triangle has two equal sides and three acute angles (less than 90°).
- Isosceles Obtuse Triangle: An isosceles obtuse triangle has two equal sides and one obtuse angle (greater than 90°).
Conclusion: A Vital Geometric Concept
The existence of a triangle that is both isosceles and right-angled is not only theoretically possible but also demonstrably true. The 45-45-90 triangle is a fundamental geometric shape with widespread practical applications across various disciplines. Understanding its properties is crucial for anyone working with geometry, trigonometry, or related fields. This exploration emphasizes the importance of precisely defining geometric concepts and the power of logical reasoning in proving geometric theorems. The 45-45-90 triangle stands as a testament to the elegant interconnectedness of geometric principles.
Latest Posts
Related Post
Thank you for visiting our website which covers about Can A Triangle Be Isosceles And Right . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.