Change The Fraction 3 4 To A Percent
News Co
Mar 18, 2025 · 5 min read
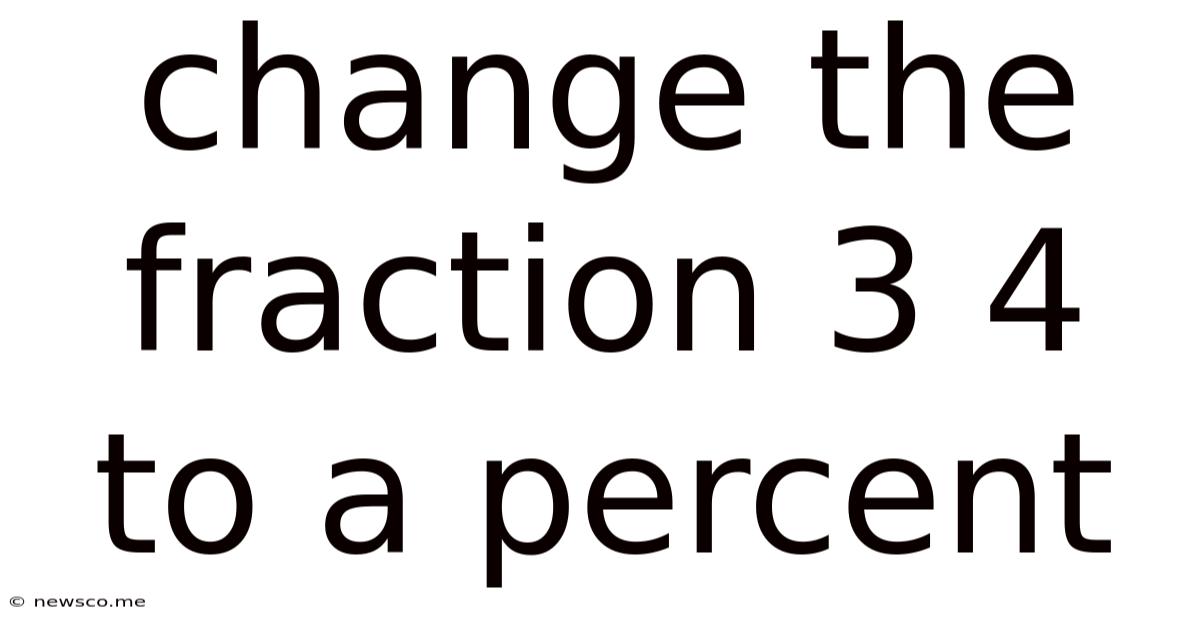
Table of Contents
Changing the Fraction 3/4 to a Percent: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with widespread applications in various fields, from everyday calculations to advanced statistical analysis. This comprehensive guide will delve into the process of converting the fraction 3/4 to a percentage, exploring different methods and providing a deeper understanding of the underlying concepts. We'll also touch upon the broader context of fraction-to-percentage conversions and their significance.
Understanding Fractions and Percentages
Before we jump into the conversion, let's solidify our understanding of fractions and percentages.
What is a Fraction?
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we have, while the denominator shows the total number of equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 parts out of a total of 4 equal parts.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Percentages are widely used because they offer a standardized way to compare different proportions. For instance, 75% means 75 parts out of 100.
Methods for Converting 3/4 to a Percentage
There are several ways to convert the fraction 3/4 to a percentage. Let's explore the most common methods:
Method 1: Using the Decimal Equivalent
This method involves first converting the fraction to a decimal and then multiplying by 100 to obtain the percentage.
-
Convert the fraction to a decimal: Divide the numerator (3) by the denominator (4): 3 ÷ 4 = 0.75
-
Multiply by 100 to express as a percentage: 0.75 x 100 = 75%
Therefore, 3/4 is equal to 75%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method relies on finding an equivalent fraction where the denominator is 100. This equivalent fraction directly represents the percentage.
-
Determine the multiplier: We need to find a number that, when multiplied by the denominator (4), results in 100. This is achieved by dividing 100 by 4: 100 ÷ 4 = 25
-
Multiply both the numerator and the denominator by the multiplier: Multiply both the numerator (3) and the denominator (4) by 25: (3 x 25) / (4 x 25) = 75/100
-
Express as a percentage: Since the denominator is 100, the numerator directly represents the percentage: 75/100 = 75%
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the percentage.
-
Set up a proportion: We can set up a proportion relating the fraction to the percentage:
3/4 = x/100
where 'x' represents the percentage we want to find.
-
Cross-multiply: Cross-multiply the terms in the proportion:
4x = 300
-
Solve for x: Divide both sides by 4:
x = 300 ÷ 4 = 75
Therefore, x = 75%
Why is Understanding this Conversion Important?
The ability to convert fractions to percentages is crucial for a variety of reasons:
-
Data Interpretation: Many datasets present data as fractions, but percentages often provide a more intuitive and easily comparable understanding. For instance, understanding that 3/4 of students passed an exam is easier to grasp when expressed as 75% passing.
-
Financial Calculations: Percentages are fundamental in finance, used for calculating interest rates, discounts, profits, and losses. Converting fractions to percentages simplifies these calculations.
-
Real-world Applications: Percentages are used everywhere, from calculating sales tax to understanding survey results, determining nutritional values in food labels, and expressing probabilities.
-
Academic Success: A solid grasp of fraction-to-percentage conversions is essential for success in mathematics and related fields.
Expanding on Fraction to Percentage Conversions: More Complex Examples
While 3/4 is a relatively straightforward example, the principles discussed above can be applied to more complex fractions. Let's look at a couple of examples:
Example 1: Converting 5/8 to a percentage
-
Convert to decimal: 5 ÷ 8 = 0.625
-
Multiply by 100: 0.625 x 100 = 62.5%
Therefore, 5/8 = 62.5%
Example 2: Converting an improper fraction to a percentage
Let's convert the improper fraction 7/4 to a percentage:
-
Convert to decimal: 7 ÷ 4 = 1.75
-
Multiply by 100: 1.75 x 100 = 175%
Note that improper fractions (where the numerator is larger than the denominator) result in percentages greater than 100%. This indicates a quantity exceeding the whole.
Example 3: Converting a mixed number to a percentage
A mixed number combines a whole number and a fraction (e.g., 2 1/2). To convert a mixed number to a percentage, first convert it to an improper fraction, then follow the steps outlined above. Let's convert 2 1/2 to a percentage:
-
Convert to an improper fraction: 2 1/2 = (2 x 2 + 1) / 2 = 5/2
-
Convert to decimal: 5 ÷ 2 = 2.5
-
Multiply by 100: 2.5 x 100 = 250%
Conclusion: Mastering Fraction-to-Percentage Conversions
Understanding how to convert fractions to percentages is a valuable skill applicable across numerous domains. The methods discussed – using decimal equivalents, equivalent fractions, and proportions – provide versatile approaches to tackle these conversions. Mastering these methods empowers you to confidently interpret data, solve problems, and navigate everyday situations involving fractions and percentages. Remember that practice is key to solidifying this skill. Try converting various fractions to percentages using the different methods to reinforce your understanding and build confidence. The more you practice, the faster and more efficient you will become.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Change The Fraction 3 4 To A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.