Common Denominator For 9 And 7
News Co
Apr 07, 2025 · 6 min read
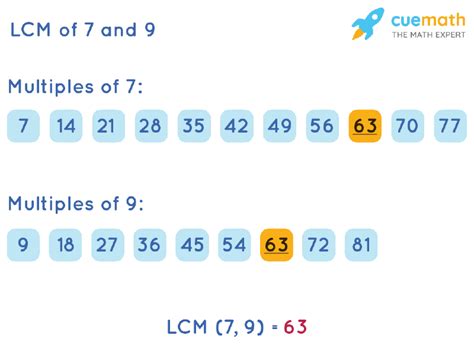
Table of Contents
Finding the Common Denominator for 9 and 7: A Deep Dive into Fractions
Finding the common denominator for two numbers, like 9 and 7, is a fundamental skill in mathematics, crucial for adding, subtracting, and comparing fractions. While seemingly simple, understanding the underlying principles can significantly improve your math skills and lay a strong foundation for more advanced concepts. This article will not only show you how to find the common denominator for 9 and 7 but will also delve into the broader context of least common multiples (LCM), greatest common divisors (GCD), and their applications in various mathematical scenarios.
Understanding Fractions and the Need for Common Denominators
A fraction represents a part of a whole. It consists of two numbers: the numerator, which indicates the number of parts we have, and the denominator, which indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator.
When adding or subtracting fractions, it's crucial that they share a common denominator. This is because you can only directly add or subtract parts that are of the same size. Imagine trying to add three quarters (3/4) and two eighths (2/8) – you can't simply add the numerators (3 + 2 = 5) and keep the denominator as it is because the sizes of the parts are different. To accurately represent the combined value, you need to express both fractions in terms of the same sized parts.
Methods for Finding the Common Denominator of 9 and 7
The common denominator for two numbers is a multiple of both numbers. For 9 and 7, we need to find a number that is divisible by both 9 and 7. Several methods can be used:
1. Listing Multiples
The simplest method is to list the multiples of each number until a common multiple is found.
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126…
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126…
Notice that 63 and 126 appear in both lists. Therefore, both 63 and 126 are common denominators for 9 and 7.
2. Prime Factorization
A more efficient method, especially for larger numbers, is to use prime factorization. Prime factorization involves expressing a number as the product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 9: 3 x 3 = 3²
- Prime factorization of 7: 7 (7 is a prime number)
To find the least common multiple (LCM), we take the highest power of each prime factor present in the factorizations:
- The LCM(9,7) = 3² x 7 = 9 x 7 = 63
Therefore, the least common multiple, and hence the least common denominator, for 9 and 7 is 63. Using the LCM ensures that you're working with the smallest possible denominator, simplifying subsequent calculations.
3. Using the Formula: LCM(a, b) = (a x b) / GCD(a, b)
This method involves finding the greatest common divisor (GCD) of the two numbers first. The GCD is the largest number that divides both numbers without leaving a remainder. For 9 and 7, the GCD is 1 because they have no common factors other than 1.
Using the formula:
LCM(9, 7) = (9 x 7) / GCD(9, 7) = (63) / 1 = 63
Again, we find that the least common denominator is 63.
Applying the Common Denominator: Adding and Subtracting Fractions
Let's illustrate how to use the common denominator (63) to add or subtract fractions with denominators 9 and 7.
Example 1: Adding Fractions
Let's add 2/9 and 3/7:
- Find the common denominator: As we've established, the LCM of 9 and 7 is 63.
- Convert the fractions:
- 2/9 = (2 x 7) / (9 x 7) = 14/63
- 3/7 = (3 x 9) / (7 x 9) = 27/63
- Add the fractions: 14/63 + 27/63 = 41/63
Therefore, 2/9 + 3/7 = 41/63
Example 2: Subtracting Fractions
Let's subtract 5/9 from 6/7:
- Find the common denominator: The LCM of 9 and 7 is 63.
- Convert the fractions:
- 6/7 = (6 x 9) / (7 x 9) = 54/63
- 5/9 = (5 x 7) / (9 x 7) = 35/63
- Subtract the fractions: 54/63 - 35/63 = 19/63
Therefore, 6/7 - 5/9 = 19/63
Beyond the Basics: Applications of LCM and GCD
The concepts of LCM and GCD extend far beyond the simple addition and subtraction of fractions. They have significant applications in various areas of mathematics and beyond:
1. Scheduling Problems
Imagine you have two events that occur at regular intervals. The LCM can help determine when both events will occur simultaneously. For example, if event A occurs every 9 days and event B occurs every 7 days, the LCM (63) tells us that both events will occur together every 63 days.
2. Modular Arithmetic and Cryptography
The GCD plays a crucial role in modular arithmetic, which is fundamental to cryptography and computer science. The Euclidean algorithm, a method for finding the GCD, is used extensively in cryptographic systems to ensure the security of encrypted data.
3. Simplifying Fractions
The GCD is used to simplify fractions to their lowest terms. For example, the fraction 12/18 can be simplified by dividing both the numerator and denominator by their GCD (6), resulting in the equivalent fraction 2/3.
4. Geometry and Measurement
LCM and GCD find applications in geometry problems related to finding common lengths or areas. They can also be used to solve problems involving the measurement of lengths, volumes, and other quantities.
5. Number Theory
LCM and GCD are fundamental concepts in number theory, a branch of mathematics dealing with the properties of integers. They are used to study various number-theoretic functions and relationships.
Conclusion: Mastering Common Denominators and Beyond
Finding the common denominator, specifically the least common denominator (LCD), for two numbers is a vital skill in mathematics. Understanding the underlying principles of LCM and GCD enhances your problem-solving abilities and opens doors to more advanced mathematical concepts. Whether you're tackling fractions, scheduling problems, or delving into the world of cryptography, mastering these fundamental concepts will significantly improve your mathematical proficiency and overall understanding of numbers and their relationships. The methods discussed – listing multiples, prime factorization, and using the LCM formula – provide diverse approaches to finding the common denominator, allowing you to choose the most efficient method based on the numbers involved. Remember, consistent practice and a clear understanding of the underlying principles are key to mastering this essential mathematical skill.
Latest Posts
Related Post
Thank you for visiting our website which covers about Common Denominator For 9 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.