Common Factors Of 12 And 9
News Co
Apr 05, 2025 · 6 min read
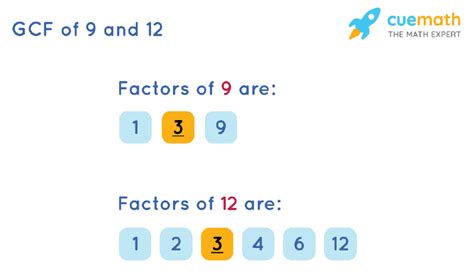
Table of Contents
Unveiling the Secrets of Common Factors: A Deep Dive into 12 and 9
Finding the common factors of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a world of mathematical beauty and practical applications. This comprehensive guide will delve into the common factors of 12 and 9, exploring the methods for finding them, their significance in number theory, and their relevance in various fields.
Understanding Factors and Common Factors
Before we embark on our journey into the fascinating world of 12 and 9, let's solidify our understanding of fundamental concepts.
Factors, also known as divisors, are whole numbers that divide evenly into a given number without leaving a remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. Each of these numbers divides 12 perfectly.
Common factors are numbers that are factors of two or more numbers. They represent the shared divisors. Let's illustrate with an example. The factors of 9 are 1, 3, and 9. Comparing the factors of 12 and 9, we see that 1 and 3 are common to both.
Methods for Finding Common Factors
Several methods exist for efficiently determining the common factors of two numbers, such as 12 and 9. We'll explore the most common and effective approaches:
1. Listing Factors
This method involves listing all the factors of each number and then identifying the common ones.
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 9: 1, 3, 9
Comparing the two lists, we find that 1 and 3 are the common factors of 12 and 9.
This method is straightforward for smaller numbers but can become cumbersome with larger numbers.
2. Prime Factorization
Prime factorization is a powerful technique based on expressing a number as a product of its prime factors. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
- Prime factorization of 12: 2 x 2 x 3 (or 2² x 3)
- Prime factorization of 9: 3 x 3 (or 3²)
By examining the prime factorizations, we identify the common prime factor: 3. Any combination of the common prime factors will also be a common factor. In this case, 3¹ (which is 3) is a common factor. Since there are no other common prime factors, 1 and 3 are the only common factors. This method becomes increasingly efficient when dealing with larger numbers.
3. Greatest Common Divisor (GCD)
The greatest common divisor (GCD), also known as the highest common factor (HCF), is the largest number that divides both numbers without leaving a remainder. The GCD of 12 and 9 is 3. All other common factors will be divisors of the GCD. Finding the GCD can be done using various methods, including:
-
Euclidean Algorithm: This efficient algorithm repeatedly applies the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- Divide 12 by 9: 12 = 1 x 9 + 3
- Divide 9 by the remainder 3: 9 = 3 x 3 + 0
The last non-zero remainder is 3, so the GCD of 12 and 9 is 3.
-
Listing Factors (as before): After identifying all common factors, the largest of these is the GCD.
Once the GCD is found, all common factors are the divisors of the GCD. Since the divisors of 3 are 1 and 3, these are the common factors of 12 and 9.
Significance of Common Factors
Understanding common factors is crucial in various mathematical contexts and real-world applications:
1. Simplifying Fractions
Common factors play a vital role in simplifying fractions. To simplify a fraction, we divide both the numerator and denominator by their greatest common factor (GCD). For example, the fraction 12/9 can be simplified to 4/3 by dividing both 12 and 9 by their GCD, which is 3.
2. Solving Equations
Common factors are essential in solving algebraic equations. Factoring expressions often requires finding common factors to simplify and solve the equation.
3. Geometry and Measurement
Common factors are used in geometry problems involving area and volume calculations. For example, finding the dimensions of the largest square tile that can perfectly cover a rectangular floor requires determining the GCD of the length and width of the floor.
4. Number Theory
Common factors are fundamental concepts in number theory, a branch of mathematics that studies the properties of integers. Concepts like coprime numbers (numbers with a GCD of 1) and relatively prime numbers rely heavily on understanding common factors.
5. Cryptography
Understanding prime factorization and GCDs is crucial in modern cryptography. Many encryption algorithms rely on the difficulty of factoring large numbers into their prime components.
Beyond the Basics: Exploring Related Concepts
The exploration of common factors opens doors to a broader understanding of number theory and related concepts. Let's briefly touch upon some of them:
1. Least Common Multiple (LCM)
While this article focuses on common factors, it's important to mention the least common multiple (LCM). The LCM is the smallest positive number that is a multiple of both numbers. The LCM of 12 and 9 is 36. The relationship between GCD and LCM is given by the formula: GCD(a, b) x LCM(a, b) = a x b. In our case, 3 x 36 = 12 x 9 = 108.
2. Relatively Prime Numbers
Two numbers are relatively prime or coprime if their greatest common divisor (GCD) is 1. For example, 12 and 35 are relatively prime because their GCD is 1.
Practical Applications in Everyday Life
While the concept of common factors might seem abstract, it finds practical applications in various aspects of daily life:
- Dividing resources equally: Imagine sharing 12 cookies and 9 candies equally among a group of friends. The largest number of friends you can share them with equally is determined by the GCD of 12 and 9, which is 3.
- Arranging objects in grids: Suppose you want to arrange 12 red balls and 9 blue balls into equal rows and columns. The largest number of balls in each row (and column) will be determined by the GCD.
- Construction and design: In construction, finding the largest common divisor is crucial when determining the dimensions of tiles or other materials for projects requiring perfect alignment.
Conclusion: The Enduring Importance of Common Factors
The seemingly simple concept of common factors reveals a rich tapestry of mathematical principles with widespread applicability. From simplifying fractions to solving complex equations and even contributing to cryptography, understanding common factors provides a strong foundation for further mathematical exploration and real-world problem-solving. By mastering the various methods for finding common factors, from basic listing to sophisticated algorithms, we gain valuable tools that enhance our numerical reasoning and contribute to a deeper appreciation of the beauty and intricacy of mathematics. The journey into the world of numbers is ongoing, and the common factors of 12 and 9 serve as a perfect starting point for this exciting adventure.
Latest Posts
Related Post
Thank you for visiting our website which covers about Common Factors Of 12 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.