Common Factors Of 21 And 30
News Co
Mar 27, 2025 · 5 min read
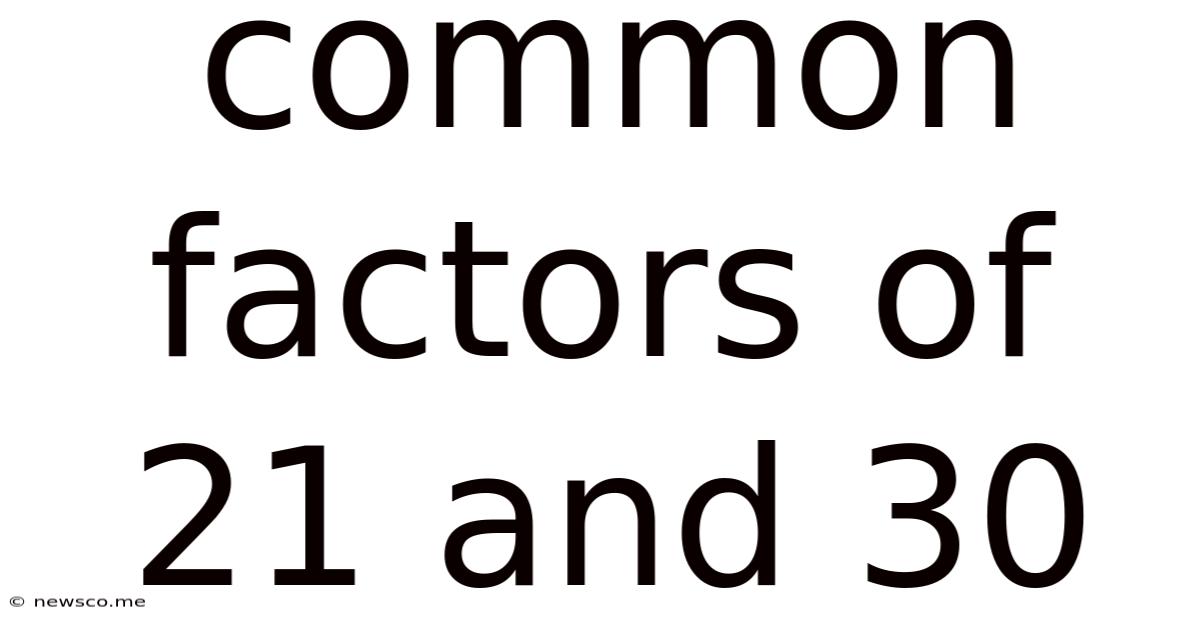
Table of Contents
Unveiling the Common Factors of 21 and 30: A Deep Dive into Number Theory
Finding the common factors of two numbers might seem like a simple arithmetic task, but it forms the bedrock of several crucial concepts in number theory and algebra. This exploration delves into the common factors of 21 and 30, expanding beyond a simple answer to uncover the underlying principles and their applications. We'll cover methods for finding these factors, explore related concepts like greatest common divisor (GCD), and even touch upon the broader implications in fields like cryptography and computer science.
Understanding Factors and Divisors
Before we jump into the specifics of 21 and 30, let's clarify the terminology. A factor (or divisor) of a number is a whole number that divides that number exactly without leaving a remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. These numbers all divide 12 evenly.
A common factor of two or more numbers is a number that is a factor of each of those numbers. Finding these common factors is the core of our investigation today.
Finding the Factors of 21 and 30
Let's begin by individually listing the factors of 21 and 30:
Factors of 21: 1, 3, 7, 21
Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
By comparing these lists, we can easily identify the common factors of 21 and 30:
Common Factors of 21 and 30: 1 and 3
These are the only whole numbers that divide both 21 and 30 without leaving a remainder.
The Greatest Common Divisor (GCD)
The greatest common divisor (GCD), also known as the highest common factor (HCF), is the largest of the common factors. In the case of 21 and 30, the GCD is 3. Understanding the GCD is crucial in many mathematical applications.
Methods for Finding the GCD
There are several methods to determine the GCD of two numbers:
-
Listing Factors: As demonstrated above, this method is straightforward for smaller numbers. However, it becomes less efficient as numbers grow larger.
-
Prime Factorization: This involves expressing each number as a product of its prime factors. The GCD is then the product of the common prime factors raised to the lowest power.
- Prime factorization of 21: 3 x 7
- Prime factorization of 30: 2 x 3 x 5
The only common prime factor is 3, therefore the GCD is 3.
-
Euclidean Algorithm: This is a highly efficient algorithm, particularly useful for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD. Let's illustrate with 21 and 30:
- 30 = 21 x 1 + 9
- 21 = 9 x 2 + 3
- 9 = 3 x 3 + 0
The last non-zero remainder is 3, so the GCD(21, 30) = 3.
Applications of Common Factors and GCD
The concept of common factors and the GCD extends far beyond simple arithmetic exercises. They have significant applications in various fields:
1. Fraction Simplification
The GCD plays a vital role in simplifying fractions. To simplify a fraction, we divide both the numerator and the denominator by their GCD. For example, the fraction 21/30 can be simplified to 7/10 by dividing both the numerator (21) and the denominator (30) by their GCD, which is 3.
2. Cryptography
Number theory, including the concepts of GCD and prime factorization, forms the foundation of many modern cryptographic systems. Algorithms like the RSA algorithm rely heavily on the difficulty of factoring large numbers into their prime factors. The security of these systems depends on the computationally intensive nature of finding the GCD of very large numbers.
3. Computer Science
The GCD is used in various computer algorithms, including those related to:
-
Data Compression: Algorithms for data compression often utilize the GCD to find common patterns and reduce redundancy.
-
Computer Graphics: The GCD can be used in algorithms for generating textures and patterns.
-
Scheduling and Resource Allocation: In operating systems and other resource-management systems, the GCD can be used to find optimal scheduling strategies.
4. Music Theory
Interestingly, the GCD finds application in music theory. The GCD of two musical intervals (measured in cents) can determine the simplest ratio representing the interval.
Beyond the Basics: Exploring Least Common Multiple (LCM)
While we've focused on the GCD, it's worth mentioning the least common multiple (LCM). The LCM is the smallest positive number that is a multiple of both numbers. For 21 and 30, the LCM is 210.
The GCD and LCM are related through the following formula:
LCM(a, b) x GCD(a, b) = a x b
In our case: LCM(21, 30) x GCD(21, 30) = 21 x 30 => 210 x 3 = 630
This relationship highlights the interconnectedness of these fundamental concepts in number theory.
Expanding the Scope: Working with Larger Numbers
While we've used 21 and 30 as our example, the principles discussed apply to any pair of integers. The Euclidean algorithm, in particular, remains highly efficient even for significantly larger numbers. This makes it a powerful tool for finding GCDs in various computational contexts.
Conclusion: The Importance of Fundamental Concepts
The seemingly simple task of finding the common factors of 21 and 30 opens a window into a rich world of mathematical concepts with wide-ranging applications. From simplifying fractions to securing sensitive data, the understanding of factors, GCDs, and related concepts forms a crucial foundation in various disciplines. By exploring these fundamental principles, we gain a deeper appreciation for the elegance and power of number theory and its impact on our technological world. This exploration goes beyond a simple answer; it reveals the interconnectedness of mathematical ideas and their practical relevance in a rapidly evolving digital landscape. Further exploration into prime factorization, modular arithmetic, and other related topics can enrich this foundational understanding and open doors to even more advanced mathematical concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about Common Factors Of 21 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.