Common Factors Of 28 And 36
News Co
Apr 05, 2025 · 6 min read
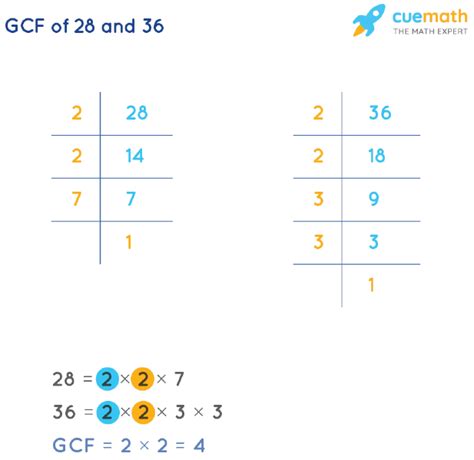
Table of Contents
Unveiling the Secrets of Common Factors: A Deep Dive into 28 and 36
Finding the common factors of two numbers might seem like a simple arithmetic task, but it's a fundamental concept with far-reaching applications in mathematics, computer science, and beyond. This article delves into the fascinating world of factors, exploring various methods to identify the common factors of 28 and 36, and then expanding on the broader significance of this seemingly simple mathematical operation. We'll cover everything from basic definitions to advanced techniques, providing a comprehensive understanding suitable for students, educators, and anyone curious about the elegance and power of number theory.
Understanding Factors and Common Factors
Before we embark on our journey to uncover the common factors of 28 and 36, let's solidify our understanding of the core concepts.
What are Factors?
A factor of a number is a whole number that divides the number exactly without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 evenly.
Identifying Factors: A Systematic Approach
There are several ways to identify the factors of a number. One common method is to systematically check each whole number, starting from 1, to see if it divides the number without a remainder. Another, more efficient approach, especially for larger numbers, is to find pairs of factors. For instance, if we find that 2 is a factor of a number, we automatically know that the number divided by 2 is also a factor.
What are Common Factors?
Common factors are numbers that are factors of two or more numbers. These are the numbers that divide both numbers without leaving a remainder. Finding the common factors helps us understand the relationships between numbers and is crucial for simplifying fractions and solving various mathematical problems.
Finding the Common Factors of 28 and 36: A Step-by-Step Guide
Now, let's focus on finding the common factors of 28 and 36. We'll use multiple methods to illustrate the various approaches available.
Method 1: Listing Factors
The simplest method involves listing all the factors of each number and then identifying the common ones.
Factors of 28: 1, 2, 4, 7, 14, 28
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
By comparing the two lists, we can see that the common factors of 28 and 36 are 1, 2, and 4.
Method 2: Prime Factorization
Prime factorization is a powerful technique that decomposes a number into its prime factors (numbers divisible only by 1 and themselves). This method is particularly useful for larger numbers.
Prime factorization of 28: 2 x 2 x 7 (or 2² x 7)
Prime factorization of 36: 2 x 2 x 3 x 3 (or 2² x 3²)
To find the common factors, we identify the prime factors that appear in both factorizations. Both 28 and 36 share two factors of 2. Therefore, the common factors are derived from the common prime factors:
- 2¹ = 2
- 2² = 4
- 2¹ x 1 = 2
- 2² x 1 = 4
- 1 (always a common factor)
Thus, the common factors are 1, 2, and 4.
Method 3: Greatest Common Divisor (GCD)
The greatest common divisor (GCD), also known as the highest common factor (HCF), is the largest number that divides both numbers without leaving a remainder. Finding the GCD provides a shortcut to finding all common factors because all other common factors will be divisors of the GCD.
There are several ways to find the GCD. One efficient method is the Euclidean algorithm. However, for smaller numbers like 28 and 36, we can use a simpler approach.
Looking at the factors listed above, we can see that the largest number that divides both 28 and 36 is 4. Therefore, the GCD of 28 and 36 is 4. All other common factors (1 and 2) are divisors of 4.
Beyond the Basics: Applications of Common Factors
Understanding common factors extends far beyond basic arithmetic. They play a vital role in various mathematical and computational applications.
Simplifying Fractions
Common factors are essential for simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and the denominator by their greatest common divisor.
For example, the fraction 28/36 can be simplified by dividing both the numerator and denominator by their GCD, which is 4:
28/36 = (28 ÷ 4) / (36 ÷ 4) = 7/9
Solving Equations
Common factors often appear in algebraic equations, particularly when factoring polynomials. Finding common factors helps simplify equations and solve for unknown variables.
Modular Arithmetic
In modular arithmetic, a branch of number theory with applications in cryptography and computer science, common factors play a critical role. The concept of congruence modulo n relies on the divisibility properties of numbers, inherently connected to the idea of common factors.
Data Structures and Algorithms
In computer science, concepts related to common factors, such as GCD calculation, are fundamental to various algorithms and data structures. For example, efficient GCD algorithms are used in cryptography and in simplifying fractions represented in computer programs.
Expanding the Concept: Least Common Multiple (LCM)
While we've focused on common factors, it's also important to understand the closely related concept of the least common multiple (LCM). The LCM of two or more numbers is the smallest number that is a multiple of all the numbers.
Finding the LCM is often used in problems involving fractions with different denominators. To add or subtract fractions with different denominators, we find the LCM of the denominators, which becomes the common denominator for the fractions. Similar to the GCD, efficient algorithms exist for calculating the LCM. The relationship between GCD and LCM is given by the formula:
LCM(a, b) = (a x b) / GCD(a, b)
Conclusion: The Enduring Importance of Common Factors
This in-depth exploration has demonstrated that while finding the common factors of 28 and 36 might seem like a simple exercise, it unveils a world of mathematical concepts with far-reaching implications. From simplifying fractions and solving equations to powering advanced algorithms in computer science, the understanding and application of common factors are fundamental to various fields. Mastering this seemingly simple concept equips you with a powerful tool for tackling a wider array of mathematical problems and strengthens your understanding of numerical relationships. The seemingly simple task of finding the common factors of 28 and 36 serves as a gateway to a much richer and more complex understanding of numbers and their interconnectedness. So, next time you encounter such a problem, remember the depth of knowledge and the diverse applications hidden within this seemingly basic mathematical operation.
Latest Posts
Related Post
Thank you for visiting our website which covers about Common Factors Of 28 And 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.