Common Factors Of 6 And 15
News Co
Apr 03, 2025 · 5 min read
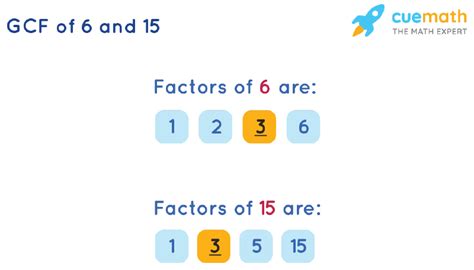
Table of Contents
Unlocking the Secrets of Numbers: A Deep Dive into the Common Factors of 6 and 15
Finding the common factors of two numbers might seem like a simple arithmetic exercise, but it's a fundamental concept that underpins a vast array of mathematical principles. This exploration delves into the common factors of 6 and 15, going beyond a simple answer to uncover the underlying concepts and their broader applications in mathematics and beyond. We'll uncover what factors are, how to find them, explore the concept of the greatest common factor (GCF), and even touch upon real-world applications.
Understanding Factors: The Building Blocks of Numbers
Before we dive into the specifics of 6 and 15, let's establish a solid understanding of what factors are. A factor of a number is a whole number that divides evenly into that number without leaving a remainder. In simpler terms, it's a number that you can multiply by another whole number to get your original number.
For example, the factors of 6 are 1, 2, 3, and 6. This is because:
- 1 x 6 = 6
- 2 x 3 = 6
Similarly, the factors of 15 are 1, 3, 5, and 15. This is because:
- 1 x 15 = 15
- 3 x 5 = 15
Identifying the Common Factors of 6 and 15
Now, let's focus on identifying the common factors of 6 and 15. These are the factors that both numbers share. By comparing the lists of factors for both numbers, we can easily identify the commonalities:
Factors of 6: 1, 2, 3, 6 Factors of 15: 1, 3, 5, 15
The numbers that appear in both lists are 1 and 3. Therefore, the common factors of 6 and 15 are 1 and 3.
Visualizing Common Factors
Visual representations can significantly enhance understanding. Consider using prime factorization to illustrate the common factors:
- Prime Factorization of 6: 2 x 3
- Prime Factorization of 15: 3 x 5
This clearly shows that the only common prime factor is 3. Since 1 is a factor of every number, we also have 1 as a common factor.
The Greatest Common Factor (GCF): Finding the Highest Commonality
While identifying common factors is important, finding the greatest common factor (GCF), also known as the highest common factor (HCF), is often even more crucial in various mathematical applications. The GCF is the largest number that divides evenly into both numbers. In the case of 6 and 15, the GCF is 3.
There are several methods to find the GCF:
-
Listing Factors: As we did above, list all the factors of each number and identify the largest one they share.
-
Prime Factorization: Find the prime factorization of each number. The GCF is the product of the common prime factors raised to the lowest power. For 6 (2 x 3) and 15 (3 x 5), the only common prime factor is 3, making the GCF 3.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF. While less intuitive for smaller numbers like 6 and 15, it becomes indispensable for larger numbers.
Applications of Common Factors and GCF: Beyond the Classroom
The seemingly simple concept of common factors and the GCF has far-reaching applications across numerous fields:
1. Simplifying Fractions:
This is perhaps the most common application. To simplify a fraction, you divide both the numerator and denominator by their GCF. For example, simplifying the fraction 6/15 involves dividing both 6 and 15 by their GCF, which is 3, resulting in the simplified fraction 2/5.
2. Solving Problems Involving Ratios and Proportions:
Understanding common factors is vital when working with ratios and proportions. Simplifying ratios to their simplest form often relies on finding the GCF.
3. Geometry and Measurement:
Finding the GCF is often used in geometry problems related to area, volume, and measurements. For instance, determining the largest square tile that can perfectly cover a rectangular floor requires finding the GCF of the floor's dimensions.
4. Number Theory:
The concept of common factors and GCF is fundamental in number theory, a branch of mathematics that studies the properties of integers.
5. Cryptography:
In cryptography, which involves securing communication, concepts related to GCF and prime factorization play a significant role in various encryption and decryption algorithms.
6. Computer Science:
Algorithms in computer science frequently utilize GCF calculations for tasks such as data compression and optimization.
Expanding Our Understanding: Exploring Related Concepts
Beyond common factors and the GCF, several related mathematical concepts build upon these foundations:
1. Least Common Multiple (LCM):
The least common multiple (LCM) is the smallest number that is a multiple of both numbers. While the GCF is the largest number that divides both numbers, the LCM is the smallest number that both numbers divide. Finding the LCM is often necessary when adding or subtracting fractions with different denominators.
2. Prime Numbers:
Understanding prime numbers – numbers greater than 1 that have only two factors, 1 and themselves – is crucial in finding factors and the GCF through prime factorization.
3. Relatively Prime Numbers:
Two numbers are relatively prime or coprime if their GCF is 1. This means they share no common factors other than 1. For example, 6 and 7 are relatively prime.
Conclusion: The Significance of Simple Concepts
While seemingly elementary, understanding common factors, the GCF, and related concepts is paramount. These foundational mathematical principles underpin countless applications in various fields, extending far beyond the typical arithmetic problems encountered in school. This deep dive into the common factors of 6 and 15 showcases how seemingly simple concepts can be rich with meaning and application, highlighting their significance in mathematics and beyond. By understanding these fundamentals, we build a strong base for tackling more complex mathematical problems and enhancing our problem-solving capabilities across numerous domains. The journey into the world of numbers, starting with the simple identification of common factors, can reveal an intricate and rewarding landscape of mathematical beauty and practicality.
Latest Posts
Related Post
Thank you for visiting our website which covers about Common Factors Of 6 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.