Common Factors Of 8 And 9
News Co
Apr 07, 2025 · 5 min read
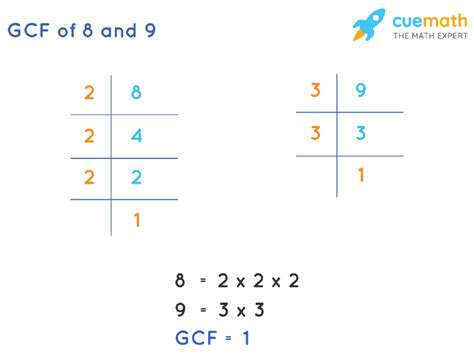
Table of Contents
Unveiling the Secrets: Common Factors of 8 and 9
Finding the common factors of two numbers might seem like a simple arithmetic task, but understanding the underlying principles reveals a deeper appreciation of number theory. This article delves into the common factors of 8 and 9, exploring the concepts of factors, prime factorization, greatest common factor (GCF), and least common multiple (LCM), and demonstrating their applications in various mathematical contexts. We’ll go beyond a simple answer, offering a comprehensive exploration suitable for both beginners and those seeking a more thorough understanding.
Understanding Factors
Before we tackle the specifics of 8 and 9, let's establish a solid foundation. A factor (or divisor) of a number is a whole number that divides the number exactly without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides 12 evenly.
It's important to distinguish between factors and multiples. Multiples are the products of a number and any whole number. For instance, multiples of 3 are 3, 6, 9, 12, and so on.
Finding the factors of a number is a fundamental skill in number theory, crucial for simplifying fractions, solving algebraic equations, and understanding more complex mathematical concepts.
Prime Factorization: The Building Blocks of Numbers
Prime factorization is a powerful technique that breaks down a number into its prime components. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11). The process of prime factorization involves expressing a number as the product of its prime factors.
Let's illustrate this with 8 and 9:
- Prime factorization of 8: 8 = 2 x 2 x 2 = 2³
- Prime factorization of 9: 9 = 3 x 3 = 3²
This decomposition into prime factors is unique for every number (except for the order of factors). This uniqueness is a cornerstone of number theory and has wide-ranging implications.
Identifying Common Factors
Now that we have the prime factorizations of 8 and 9, we can easily identify their common factors. A common factor is a number that divides both numbers without leaving a remainder. By comparing the prime factorizations, we look for prime factors present in both numbers.
Comparing 2³ (8) and 3² (9), we observe that there are no common prime factors. This means that the only common factor of 8 and 9 is 1. This is because 1 is a factor of every whole number.
Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the highest common factor (HCF), is the largest number that divides both numbers without leaving a remainder. In our case, since the only common factor of 8 and 9 is 1, the GCF(8, 9) = 1.
The GCF is important in various mathematical applications, including:
- Simplifying fractions: The GCF allows you to reduce a fraction to its simplest form. For example, the fraction 12/18 can be simplified by dividing both the numerator and denominator by their GCF (6), resulting in 2/3.
- Solving equations: The GCF can be used to simplify algebraic expressions and equations.
- Geometry: The GCF can be used to find the dimensions of the largest square that can be used to tile a rectangle.
Least Common Multiple (LCM)
While we’re focusing on common factors, it's worth briefly mentioning the least common multiple (LCM). The LCM is the smallest positive number that is a multiple of both numbers.
To find the LCM of 8 and 9, we can use their prime factorizations:
- 8 = 2³
- 9 = 3²
Since there are no common prime factors, the LCM is simply the product of the highest powers of all prime factors present in either number: LCM(8, 9) = 2³ x 3² = 8 x 9 = 72
Applications in Real-World Scenarios
The concepts of factors, GCF, and LCM are not just abstract mathematical notions; they have practical applications in various real-world situations:
- Dividing resources: Imagine you have 8 apples and 9 oranges. You want to divide them into identical groups, with each group having the same number of apples and oranges. The GCF (1) tells you that you can only create groups of 1.
- Scheduling events: If event A occurs every 8 days and event B occurs every 9 days, the LCM (72) helps determine when both events will occur on the same day again.
- Measurement conversions: Converting units of measurement often involves finding common factors and multiples. For example, converting inches to feet requires understanding the relationship between these units, which involves factors and multiples.
Expanding the Understanding: Beyond 8 and 9
While we’ve thoroughly explored the common factors of 8 and 9, the principles discussed can be applied to any pair of numbers. Understanding the process of prime factorization and how to find the GCF and LCM is essential for many areas of mathematics.
For instance, let's consider finding the common factors of 12 and 18:
- Prime factorization of 12: 2² x 3
- Prime factorization of 18: 2 x 3²
The common prime factors are 2 and 3. Therefore, the common factors are 1, 2, 3, and 6. The GCF(12, 18) = 6.
Conclusion: The Significance of Common Factors
This in-depth exploration of the common factors of 8 and 9 has demonstrated the fundamental importance of understanding factors, prime factorization, GCF, and LCM in mathematics. These concepts are not just theoretical; they are crucial tools for solving problems in various fields, from simplifying fractions to scheduling events. By mastering these concepts, you gain a deeper appreciation for the structure and beauty of numbers and their applications in the real world. Remember that the seemingly simple task of finding common factors opens the door to a vast world of mathematical possibilities. Continue exploring, experimenting, and discovering the fascinating intricacies of number theory!
Latest Posts
Latest Posts
-
How Many Ml In Half Cup
Apr 09, 2025
-
Lcm Of 3 6 And 4
Apr 09, 2025
-
How To Find A Particular Solution
Apr 09, 2025
-
How Many Bottles Are In A Gallon
Apr 09, 2025
-
Least Common Multiple 7 And 14
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Common Factors Of 8 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.