Complete The Square X2 6x 13
News Co
May 09, 2025 · 6 min read
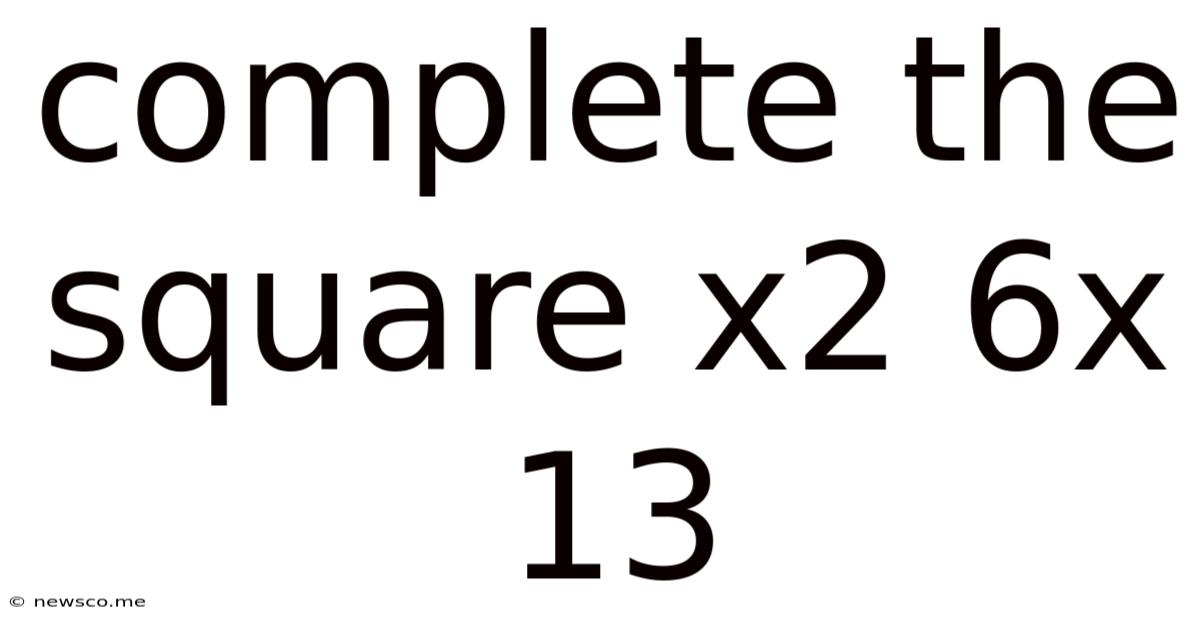
Table of Contents
Completing the Square: A Comprehensive Guide to Solving x² + 6x + 13 = 0
Completing the square is a valuable algebraic technique used to solve quadratic equations, rewrite quadratic functions in vertex form, and simplify various mathematical expressions. This comprehensive guide will delve into the process of completing the square, specifically focusing on the equation x² + 6x + 13 = 0, demonstrating the method step-by-step and exploring its broader applications.
Understanding Quadratic Equations
Before we embark on completing the square, let's refresh our understanding of quadratic equations. A quadratic equation is an equation of the form ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. The solutions to a quadratic equation are the values of 'x' that satisfy the equation. These solutions are also known as the roots or zeros of the equation. We can solve quadratic equations using various methods, including factoring, the quadratic formula, and completing the square. Each method offers its own advantages and is best suited for different types of quadratic equations.
Completing the Square: The Process
Completing the square involves manipulating a quadratic expression to create a perfect square trinomial. A perfect square trinomial is a trinomial that can be factored into the square of a binomial. The general form of a perfect square trinomial is a² + 2ab + b² = (a + b)². The key to completing the square lies in identifying the value needed to transform the given quadratic expression into a perfect square trinomial.
Let's apply this to our example: x² + 6x + 13 = 0.
Step 1: Isolate the x terms:
The first step is to isolate the terms containing 'x'. In our equation, we want to move the constant term (13) to the right side of the equation:
x² + 6x = -13
Step 2: Identify 'b' and find (b/2)²:
In our equation, the coefficient of 'x' (b) is 6. We need to find (b/2)²:
(6/2)² = 3² = 9
Step 3: Add (b/2)² to both sides:
This is the crucial step where we "complete the square." We add 9 to both sides of the equation to maintain balance:
x² + 6x + 9 = -13 + 9
Step 4: Factor the perfect square trinomial:
The left side of the equation is now a perfect square trinomial, which can be factored as (x + 3)²:
(x + 3)² = -4
Step 5: Solve for x:
To solve for 'x', we take the square root of both sides:
√(x + 3)² = ±√(-4)
x + 3 = ±2i (since the square root of a negative number is an imaginary number)
Step 6: Isolate x:
Finally, we isolate 'x' by subtracting 3 from both sides:
x = -3 ± 2i
Therefore, the solutions to the equation x² + 6x + 13 = 0 are x = -3 + 2i and x = -3 - 2i. These are complex conjugate solutions.
Interpreting Complex Solutions
The presence of imaginary numbers (i, where i² = -1) in the solutions indicates that the parabola represented by the quadratic equation does not intersect the x-axis. In other words, the quadratic equation has no real roots. The complex solutions represent the points where the parabola would intersect the complex plane.
Geometric Interpretation of Completing the Square
Completing the square also has a significant geometric interpretation. Consider the quadratic function y = x² + 6x + 13. Completing the square transforms this equation into vertex form: y = (x + 3)² + 4. This form reveals the vertex of the parabola, which is (-3, 4). The process of completing the square effectively translates the parabola to its vertex form, making it easier to analyze its key features.
Vertex Form and its Significance
The vertex form, y = a(x - h)² + k, where (h, k) represents the vertex, is incredibly useful for graphing quadratic functions. It quickly identifies the vertex, the axis of symmetry (x = h), and the direction of the parabola (opens upwards if 'a' is positive, downwards if 'a' is negative).
Applications of Completing the Square
Completing the square is not limited to solving quadratic equations. It has several important applications in various mathematical contexts:
1. Graphing Quadratic Functions
As demonstrated earlier, completing the square allows us to easily identify the vertex and other key features of a quadratic function, enabling us to accurately graph the parabola.
2. Calculus
Completing the square is frequently used in calculus to simplify integrals and derivatives involving quadratic expressions. It simplifies calculations and facilitates the application of integration techniques.
3. Solving Quadratic Inequalities
Completing the square can be extended to solve quadratic inequalities. By transforming the inequality into vertex form, we can determine the intervals where the quadratic expression is positive or negative.
4. Derivation of the Quadratic Formula
The quadratic formula itself can be derived using the method of completing the square. This derivation provides a deeper understanding of the formula's origins and its connection to the underlying algebraic manipulations.
5. Solving Certain Types of Equations
Completing the square can be used to solve equations that are not explicitly quadratic but can be manipulated into a quadratic form. This expands the applicability of the technique to a wider range of equations.
Alternative Methods for Solving Quadratic Equations
While completing the square is a powerful technique, it's essential to acknowledge other methods for solving quadratic equations:
1. Factoring
Factoring is a straightforward method applicable to quadratic equations that can be factored easily. However, not all quadratic equations are easily factorable.
2. Quadratic Formula
The quadratic formula, x = [-b ± √(b² - 4ac)] / 2a, provides a general solution for any quadratic equation. It's a reliable method, but it can be computationally more intensive than completing the square in certain cases.
Choosing the Right Method
The choice of method for solving a quadratic equation depends on the specific equation and the context of the problem. If the equation is easily factorable, factoring is the most efficient method. If the equation is not easily factorable but has a simple structure, completing the square might be preferable. For complex or general quadratic equations, the quadratic formula is the most reliable option.
Conclusion
Completing the square is a fundamental algebraic technique with wide-ranging applications beyond simply solving quadratic equations. Its geometric interpretation, its usefulness in transforming quadratic functions into vertex form, and its role in simplifying various mathematical expressions solidify its importance in algebra and beyond. While other methods exist, understanding and mastering completing the square provides a robust and versatile tool for tackling various mathematical challenges. Through this comprehensive guide, we’ve not only solved x² + 6x + 13 = 0 but also explored the broader significance and applications of this powerful algebraic method. Remember to practice regularly to develop proficiency and appreciate the elegance and power of completing the square.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Complete The Square X2 6x 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.