Definition Of Addition Property Of Equality In Math
News Co
Apr 06, 2025 · 5 min read
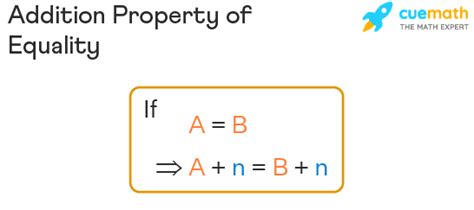
Table of Contents
The Addition Property of Equality: A Comprehensive Guide
The addition property of equality is a fundamental concept in algebra and mathematics at large. Understanding it is crucial for solving equations and manipulating algebraic expressions. This comprehensive guide will delve deep into its definition, applications, practical examples, and related properties, ensuring you gain a thorough understanding of this essential mathematical principle.
What is the Addition Property of Equality?
The Addition Property of Equality states that if you add the same number to both sides of an equation, the equation remains true. This seemingly simple statement underpins a vast amount of algebraic manipulation and problem-solving. More formally:
If a = b, then a + c = b + c, where 'a', 'b', and 'c' represent any numbers (real numbers, integers, etc.).
This property works because adding the same quantity to both sides maintains the balance of the equation. Think of it like a seesaw: if both sides are balanced, adding the same weight to each side keeps the seesaw balanced. The equation remains equal.
Understanding the "Why" Behind the Property
The Addition Property of Equality stems directly from the axioms of equality. These axioms are fundamental assumptions upon which the entire structure of algebra is built. Key axioms supporting this property include:
- Reflexive Property: A quantity is equal to itself (a = a).
- Symmetric Property: If a = b, then b = a.
- Transitive Property: If a = b and b = c, then a = c.
The Addition Property can be derived logically from these axioms. By adding a constant to both sides, we aren't changing the inherent relationship between 'a' and 'b'; we're simply transforming the equation while preserving its equality.
Practical Applications and Examples
The Addition Property of Equality is used extensively in solving algebraic equations. Consider the following examples:
Example 1: Solving a Simple Equation
Solve for x: x - 5 = 10
To isolate 'x', we need to eliminate the '-5'. Using the Addition Property, we add 5 to both sides:
x - 5 + 5 = 10 + 5
This simplifies to:
x = 15
Example 2: Equations with Fractions
Solve for y: y - (1/2) = 3/4
Adding (1/2) to both sides:
y - (1/2) + (1/2) = 3/4 + (1/2)
y = 3/4 + 2/4
y = 5/4 or 1.25
Example 3: Equations with Variables on Both Sides
Solve for z: 2z + 3 = z + 7
To isolate 'z', we can subtract 'z' from both sides (which is essentially adding '-z'):
2z + 3 - z = z + 7 - z
This simplifies to:
z + 3 = 7
Subtracting 3 from both sides (using the Subtraction Property, which is closely related):
z = 4
Example 4: Real-World Application
Imagine you're tracking your savings. You started with $20 and added 'x' dollars. You now have $50. The equation is:
20 + x = 50
Subtracting 20 from both sides (using the subtraction property of equality), you find:
x = 30. You added $30 to your savings.
The Subtraction Property of Equality: A Close Relative
The Subtraction Property of Equality is essentially a corollary of the Addition Property. It states that if you subtract the same number from both sides of an equation, the equation remains true.
If a = b, then a - c = b - c
It works on the same principle of maintaining balance. Subtracting a number is the same as adding its negative counterpart. Therefore, the Subtraction Property is implicitly covered by the Addition Property.
Connecting to Other Properties of Equality
The Addition and Subtraction properties are part of a family of properties that allow us to manipulate equations while preserving their equality. These include:
- Multiplication Property of Equality: If a = b, then a * c = b * c (Multiplying both sides by the same non-zero number).
- Division Property of Equality: If a = b and c ≠ 0, then a / c = b / c (Dividing both sides by the same non-zero number).
These properties work in conjunction with each other. Often, solving a complex equation requires using several of these properties in sequence.
Advanced Applications and Extensions
The Addition Property extends beyond simple linear equations. It's fundamental to:
- Solving systems of equations: Techniques like elimination often involve adding or subtracting equations to eliminate variables.
- Working with inequalities: While the rules are slightly modified for inequalities (e.g., multiplying by a negative number requires flipping the inequality sign), the core principle of adding the same quantity to both sides remains crucial.
- Matrix algebra: The concept of adding matrices relies on the same principle of adding corresponding elements, maintaining equality.
Common Mistakes to Avoid
While the Addition Property of Equality is straightforward, some common mistakes can occur:
- Incorrect application: Adding or subtracting a number from only one side of the equation will lead to an incorrect result. It's crucial to maintain the balance by performing the operation on both sides.
- Errors in arithmetic: Simple arithmetic mistakes can derail the entire process. Carefully check your calculations at each step.
- Confusing addition and subtraction: Ensure you're correctly applying addition or subtraction to isolate the variable.
Mastering the Addition Property: Practice Makes Perfect
The best way to truly grasp the Addition Property of Equality is through practice. Solve a variety of equations, starting with simple ones and gradually progressing to more complex ones. Work through examples that incorporate fractions, decimals, and variables on both sides of the equation. This consistent practice will build your confidence and understanding of this fundamental mathematical concept.
Conclusion
The Addition Property of Equality is a cornerstone of algebra. Its simplicity belies its power and far-reaching applications. By understanding its definition, applications, and relationship to other properties of equality, you'll be well-equipped to tackle a wide range of mathematical problems and unlock a deeper appreciation for the elegance and logic underpinning algebra. Remember, consistent practice is key to mastering this essential skill.
Latest Posts
Related Post
Thank you for visiting our website which covers about Definition Of Addition Property Of Equality In Math . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.