Derivative Of 1 Square Root X
News Co
Apr 05, 2025 · 6 min read
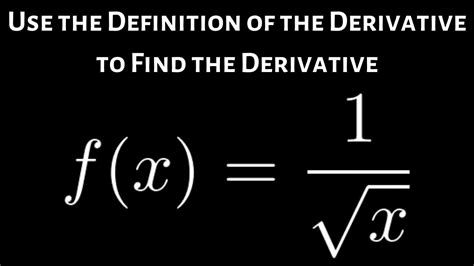
Table of Contents
Delving Deep into the Derivative of √x: A Comprehensive Guide
The derivative of √x, or x<sup>1/2</sup>, is a fundamental concept in calculus with widespread applications across various fields. This comprehensive guide will explore this derivative in detail, covering its derivation, applications, and related concepts. We will go beyond a simple answer, providing a thorough understanding to equip you with the tools to tackle more complex problems.
Understanding the Basics: Functions and Derivatives
Before diving into the derivative of √x, let's refresh our understanding of fundamental concepts.
What is a Function?
A function, in mathematical terms, is a relationship between a set of inputs (the domain) and a set of possible outputs (the codomain) with the property that each input is related to exactly one output. We often represent functions using notation like f(x), where x represents the input and f(x) represents the corresponding output. For example, f(x) = √x is a function that maps a non-negative real number x to its square root.
What is a Derivative?
The derivative of a function represents the instantaneous rate of change of that function with respect to its input. Geometrically, it represents the slope of the tangent line to the function's graph at a given point. The process of finding a derivative is called differentiation.
We use various notations to represent the derivative, including:
- f'(x) (pronounced "f prime of x")
- dy/dx (pronounced "dy by dx")
- df(x)/dx (pronounced "df of x by dx")
These all denote the same thing: the derivative of the function with respect to x.
Deriving the Derivative of √x using the Power Rule
The most straightforward method to find the derivative of √x is to use the power rule of differentiation. This rule states that the derivative of x<sup>n</sup> is nx<sup>n-1</sup>, where 'n' is any real number.
First, we rewrite √x as x<sup>1/2</sup>. Now, applying the power rule:
d/dx (x<sup>1/2</sup>) = (1/2)x<sup>(1/2)-1</sup> = (1/2)x<sup>-1/2</sup>
This can be simplified further:
(1/2)x<sup>-1/2</sup> = 1 / (2x<sup>1/2</sup>) = 1 / (2√x)
Therefore, the derivative of √x is 1 / (2√x).
Understanding the Result: Implications and Interpretation
The derivative, 1 / (2√x), tells us several important things about the function √x:
-
Rate of Change: The derivative represents the instantaneous rate of change of the square root function at any given point x. Notice that the rate of change is inversely proportional to the square root of x. As x increases, the rate of change decreases, indicating that the function grows slower as x gets larger.
-
Slope of the Tangent: At any point on the graph of y = √x, the slope of the tangent line to the curve is given by 1 / (2√x).
-
Domain Restrictions: The derivative 1 / (2√x) is undefined at x = 0 because we cannot divide by zero. This reflects the fact that the function √x is not differentiable at x = 0; the graph has a vertical tangent at that point. The domain of the derivative is (0, ∞).
Alternative Methods for Finding the Derivative
While the power rule offers the most efficient approach, we can explore alternative methods to demonstrate a deeper understanding of the underlying principles.
Using the Limit Definition of the Derivative
The derivative can be defined using limits:
f'(x) = lim<sub>h→0</sub> [(f(x+h) - f(x))/h]
Let's apply this definition to f(x) = √x:
f'(x) = lim<sub>h→0</sub> [(√(x+h) - √x)/h]
To evaluate this limit, we can use the conjugate:
f'(x) = lim<sub>h→0</sub> [(√(x+h) - √x)/h] * [(√(x+h) + √x)/(√(x+h) + √x)]
This simplifies to:
f'(x) = lim<sub>h→0</sub> [(x+h - x) / (h(√(x+h) + √x))] = lim<sub>h→0</sub> [h / (h(√(x+h) + √x))]
Cancelling the 'h' terms and evaluating the limit as h approaches 0:
f'(x) = 1 / (2√x)
This method, although more complex, reinforces the fundamental definition of the derivative.
Applications of the Derivative of √x
The derivative of √x has numerous applications in various fields, including:
Physics:
-
Velocity and Acceleration: If √x represents the displacement of an object, its derivative, 1/(2√x), represents its velocity. The derivative of velocity, which is the second derivative of displacement, represents acceleration.
-
Optics: The derivative is used in calculations related to the refractive index and lens design.
Economics and Finance:
-
Marginal Cost/Revenue: If √x represents a cost or revenue function, its derivative gives the marginal cost or revenue, the rate of change of cost or revenue with respect to the quantity produced or sold.
-
Optimization Problems: The derivative is used to find the maximum or minimum values of functions, enabling the optimization of various economic models.
Engineering:
-
Curve Design: The derivative is crucial in designing curves for roads, railways, and other engineering applications.
-
Fluid Dynamics: The derivative is used extensively in equations describing the flow of fluids.
Computer Science:
- Algorithm Analysis: Derivatives are used to analyze the efficiency of algorithms. For example, understanding the rate of growth of an algorithm's runtime.
Higher-Order Derivatives of √x
We can also calculate higher-order derivatives. The second derivative, denoted as f''(x) or d²y/dx², represents the rate of change of the first derivative.
For f(x) = √x, the first derivative is f'(x) = 1/(2√x). Therefore:
f''(x) = d/dx (1/(2√x)) = d/dx (1/2 x<sup>-1/2</sup>) = -1/4 x<sup>-3/2</sup> = -1/(4x√x)
Similarly, we can find the third derivative, fourth derivative, and so on. Each successive derivative provides further information about the behavior of the function and its rate of change.
Conclusion: Mastering the Derivative of √x
Understanding the derivative of √x—and the methods used to derive it—is crucial for anyone studying calculus. Its simplicity belies its significance, serving as a cornerstone for more advanced mathematical concepts and providing a powerful tool for solving real-world problems across diverse disciplines. By grasping the underlying principles and exploring the various applications, you equip yourself with a robust foundation for further exploration in mathematics and its related fields. Remember the key result: the derivative of √x is 1/(2√x), and understanding why this is the case allows you to apply this knowledge effectively in various scenarios. This comprehensive guide provided not just the answer, but the understanding to confidently tackle more complex derivatives in the future.
Latest Posts
Related Post
Thank you for visiting our website which covers about Derivative Of 1 Square Root X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.