Derivative Of X Sin X + Cos X
News Co
May 07, 2025 · 5 min read
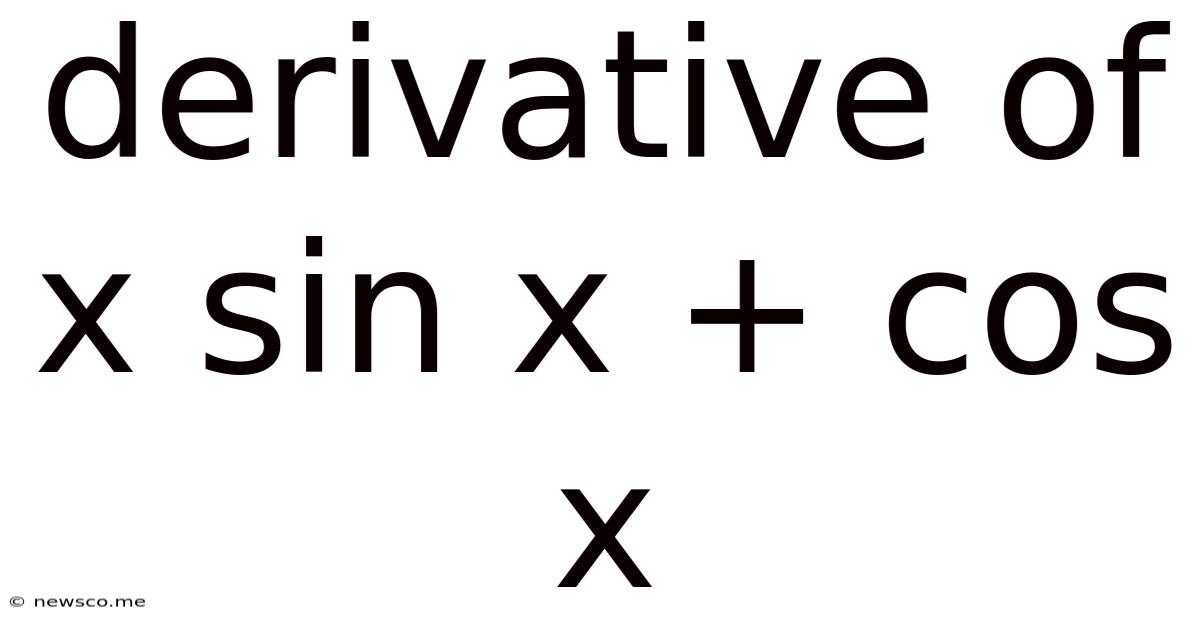
Table of Contents
Finding the Derivative of x sin x + cos x: A Comprehensive Guide
Finding the derivative of a function is a fundamental concept in calculus. This article will provide a detailed explanation of how to derive the derivative of the function f(x) = x sin x + cos x, covering various approaches and related concepts. We'll explore the necessary rules of differentiation, step-by-step calculations, and applications. This comprehensive guide aims to build a strong understanding of the process, useful for students and anyone interested in improving their calculus skills.
Understanding the Building Blocks: Differentiation Rules
Before diving into the derivation of x sin x + cos x, let's review the essential rules of differentiation we'll be using:
1. The Power Rule:
The power rule states that the derivative of x<sup>n</sup> is nx<sup>n-1</sup>, where n is a constant. For example, the derivative of x² is 2x, and the derivative of x³ is 3x².
2. The Product Rule:
The product rule is crucial when dealing with functions multiplied together. If we have a function h(x) = f(x)g(x), then its derivative is given by:
h'(x) = f'(x)g(x) + f(x)g'(x)
In simpler terms, the derivative of a product is the derivative of the first function times the second, plus the first function times the derivative of the second.
3. The Sum/Difference Rule:
The derivative of a sum (or difference) of functions is simply the sum (or difference) of their derivatives. If h(x) = f(x) ± g(x), then h'(x) = f'(x) ± g'(x).
4. Derivatives of Trigonometric Functions:
The derivatives of the basic trigonometric functions are essential for this problem:
- d(sin x)/dx = cos x
- d(cos x)/dx = -sin x
Step-by-Step Derivation of the Derivative
Now, let's tackle the derivative of f(x) = x sin x + cos x. We'll apply the rules discussed above:
First, we can separate the function into two parts:
- g(x) = x sin x
- h(x) = cos x
We'll find the derivative of each part individually and then combine them using the sum rule.
1. Finding the derivative of g(x) = x sin x:
This requires the product rule, where f(x) = x and g(x) = sin x.
- f'(x) = 1 (derivative of x)
- g'(x) = cos x (derivative of sin x)
Applying the product rule:
g'(x) = f'(x)g(x) + f(x)g'(x) = 1 * sin x + x * cos x = sin x + x cos x
2. Finding the derivative of h(x) = cos x:
This is a straightforward application of the derivative of the cosine function:
h'(x) = -sin x
3. Combining the Derivatives:
Now, we combine the derivatives of g(x) and h(x) using the sum rule:
f'(x) = g'(x) + h'(x) = (sin x + x cos x) + (-sin x) = x cos x
Therefore, the derivative of f(x) = x sin x + cos x is x cos x.
Verifying the Result Using Numerical Methods
While the analytical derivation above provides a precise answer, we can use numerical methods to verify our result. Numerical differentiation approximates the derivative using small changes in the input. This isn't as precise as the analytical method but serves as a useful check. Several techniques exist, including finite difference methods (forward, backward, central difference). For example, using the central difference method:
f'(x) ≈ [f(x + Δx) - f(x - Δx)] / (2Δx)
Where Δx is a small increment. By choosing a sufficiently small Δx and comparing the result to our analytical derivative (x cos x), we can gain confidence in our solution. However, remember that numerical methods introduce approximation errors.
Applications and Significance
The derivative of x sin x + cos x, being x cos x, finds applications in various fields:
-
Physics: This type of function and its derivative often appear in oscillatory systems, wave mechanics, and the analysis of simple harmonic motion. The derivative represents the instantaneous rate of change of the function, which can be crucial for understanding the velocity and acceleration of an oscillating object.
-
Engineering: In electrical engineering, similar functions might model alternating currents or voltages. The derivative helps in calculating the instantaneous rate of change of these quantities. In mechanical engineering, oscillatory systems, such as spring-mass systems, are also modeled with similar functions.
-
Signal Processing: The derivative plays a critical role in signal processing, where it can be used to identify edges, discontinuities, and other important features in signals. Functions related to x sin x + cos x can represent various waveforms encountered in signal processing.
Exploring Related Concepts and Further Learning
Understanding the derivative of x sin x + cos x provides a strong foundation for exploring more advanced concepts in calculus:
-
Higher-Order Derivatives: We can further differentiate x cos x to find the second, third, and higher-order derivatives. This is essential for understanding the curvature and other properties of the original function.
-
Taylor and Maclaurin Series: These series expansions use derivatives to approximate functions. Understanding the derivatives of trigonometric functions is crucial for understanding the Taylor and Maclaurin series expansions of trigonometric functions.
-
Differential Equations: Differential equations often involve derivatives, and understanding how to find derivatives is fundamental to solving these equations. Many physical systems are modeled using differential equations involving trigonometric functions.
-
Applications in other fields: The concepts explored here extend to areas beyond the typical calculus applications, appearing in areas such as computer graphics, image processing, and financial modeling, albeit often in more complex forms.
Conclusion
This comprehensive guide has thoroughly explained the process of finding the derivative of x sin x + cos x, emphasizing the application of fundamental rules of differentiation. We've demonstrated the step-by-step calculation, verified the result using numerical methods, and highlighted the significance of this derivative in diverse fields. By mastering this concept, you’ll build a robust foundation for more advanced topics in calculus and its applications in science, engineering, and other quantitative disciplines. Remember that practice is key to mastering calculus; applying these concepts to diverse problems will solidify your understanding and improve your problem-solving skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about Derivative Of X Sin X + Cos X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.