Do Vertical Angles Add Up To 180
News Co
Apr 05, 2025 · 5 min read
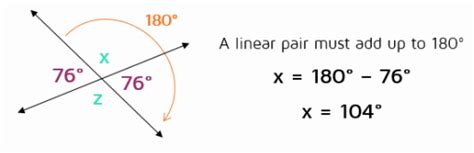
Table of Contents
Do Vertical Angles Add Up to 180 Degrees? Exploring Angle Relationships
The question, "Do vertical angles add up to 180 degrees?" is a common point of confusion in geometry. The short answer is no, vertical angles do not add up to 180 degrees. However, they do share a crucial relationship, and understanding this relationship is key to mastering various geometric proofs and problem-solving scenarios. This article delves deep into the properties of vertical angles, linear pairs, and how they interact to form the foundation of many geometric concepts.
Understanding Vertical Angles
Before we debunk the misconception, let's define what vertical angles actually are. Vertical angles are the angles opposite each other when two lines intersect. Imagine two straight lines crossing like an "X." The angles formed directly across from each other are vertical angles. They share a common vertex (the point where the lines intersect), but they don't share any common sides.
Key characteristics of vertical angles:
- They are always congruent: This is the crucial fact. Congruent means they have the same measure. If one vertical angle measures 45 degrees, its vertical angle also measures 45 degrees.
- They are formed by intersecting lines: Without intersecting lines, you cannot have vertical angles.
- They are non-adjacent: Vertical angles do not share a common side. Adjacent angles, on the other hand, share a common side and vertex.
Linear Pairs and Their 180-Degree Relationship
The confusion about vertical angles summing to 180 degrees often arises from their relationship with linear pairs. A linear pair consists of two adjacent angles formed by intersecting lines that share a common side and whose non-common sides form a straight line. Crucially, linear pairs do add up to 180 degrees. This is because a straight line represents a 180-degree angle.
Key characteristics of linear pairs:
- They are adjacent: They share a common side and vertex.
- Their non-common sides form a straight line: This is the defining characteristic of a linear pair.
- They are supplementary: Supplementary angles are two angles whose sum is 180 degrees. All linear pairs are supplementary.
The Relationship Between Vertical Angles and Linear Pairs
Here's where the connection and the distinction become clear. When two lines intersect, they form two pairs of vertical angles and four linear pairs. Each vertical angle forms a linear pair with its adjacent angle. Because the linear pair sums to 180 degrees, we can deduce the measure of the vertical angle.
Let's illustrate this with an example:
Suppose we have two intersecting lines. Let's call the vertical angles ∠A and ∠B. ∠A and ∠B are vertical angles, therefore they are congruent (∠A = ∠B). ∠A forms a linear pair with an adjacent angle, let's call it ∠C. Since ∠A and ∠C form a linear pair, their sum is 180 degrees (∠A + ∠C = 180°).
Similarly, ∠B forms a linear pair with an adjacent angle, let's call it ∠D (∠B + ∠D = 180°). Because ∠A = ∠B, it follows that ∠C and ∠D must also be equal (∠C = ∠D). ∠C and ∠D are also vertical angles.
Proving the Congruence of Vertical Angles
We can formally prove that vertical angles are always congruent using the following steps:
-
Start with intersecting lines: Draw two intersecting lines forming four angles: ∠1, ∠2, ∠3, and ∠4. ∠1 and ∠2 are adjacent angles; ∠2 and ∠3 are adjacent angles; and so on.
-
Identify linear pairs: ∠1 and ∠2 form a linear pair, as do ∠2 and ∠3, ∠3 and ∠4, and ∠4 and ∠1.
-
Use the supplementary angle property: Since linear pairs are supplementary, we can write the following equations:
- ∠1 + ∠2 = 180°
- ∠2 + ∠3 = 180°
-
Solve for equality: Since both equations equal 180°, we can set them equal to each other:
- ∠1 + ∠2 = ∠2 + ∠3
-
Subtract the common angle: Subtract ∠2 from both sides of the equation:
- ∠1 = ∠3
This proves that ∠1 and ∠3, which are vertical angles, are congruent. The same logic can be applied to prove that ∠2 and ∠4 are also congruent.
Common Mistakes and Misconceptions
The most common mistake is confusing vertical angles with linear pairs. Remember:
- Vertical angles are congruent (equal in measure).
- Linear pairs are supplementary (add up to 180°).
Another misconception is assuming that any two angles that appear opposite each other are vertical angles. They must be formed by intersecting lines.
Applications of Vertical Angles in Geometry
Understanding vertical angles is fundamental to various geometrical problems and proofs. They are frequently used in:
- Solving for unknown angles: If you know the measure of one vertical angle, you automatically know the measure of its opposite angle.
- Geometric constructions: Vertical angles play a role in constructions involving bisecting angles and constructing perpendicular lines.
- Proving geometric theorems: Numerous geometric theorems rely on the properties of vertical angles and linear pairs for their proofs. Understanding these relationships is crucial for successfully navigating more advanced geometrical concepts.
Expanding on Angle Relationships: Adjacent Angles, Complementary Angles, and More
While vertical and linear pairs are central, several other angle relationships enrich our geometric understanding. Let's briefly explore some of these:
Adjacent Angles: As mentioned earlier, adjacent angles share a common vertex and side. Their measures are not necessarily related, except in the specific case of linear pairs.
Complementary Angles: Two angles are complementary if their sum equals 90 degrees. Unlike linear pairs, complementary angles don't have to be adjacent.
Supplementary Angles: As we've seen, supplementary angles add up to 180 degrees. Linear pairs are a subset of supplementary angles.
Acute, Obtuse, Right, and Straight Angles: These classifications categorize angles based on their measures:
- Acute: Less than 90 degrees.
- Right: Exactly 90 degrees.
- Obtuse: Greater than 90 degrees but less than 180 degrees.
- Straight: Exactly 180 degrees.
Mastering these angle relationships provides a solid foundation for tackling complex geometry problems.
Conclusion: Vertical Angles – Congruent, Not Supplementary
To reiterate, vertical angles do not add up to 180 degrees. They are congruent, meaning they have equal measures. The 180-degree relationship applies to linear pairs, which are adjacent angles that form a straight line. Understanding the difference between vertical angles and linear pairs is crucial for success in geometry. By grasping these fundamental concepts and their interconnectedness, you'll be well-equipped to tackle more complex geometric problems and proofs confidently. Remember to practice identifying these angles in various diagrams and applying the properties to solve for unknown angles. This practice solidifies your understanding and prepares you for more advanced geometric concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about Do Vertical Angles Add Up To 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.