Does 1/3 And 1/3 Make 2/3
News Co
Mar 25, 2025 · 5 min read
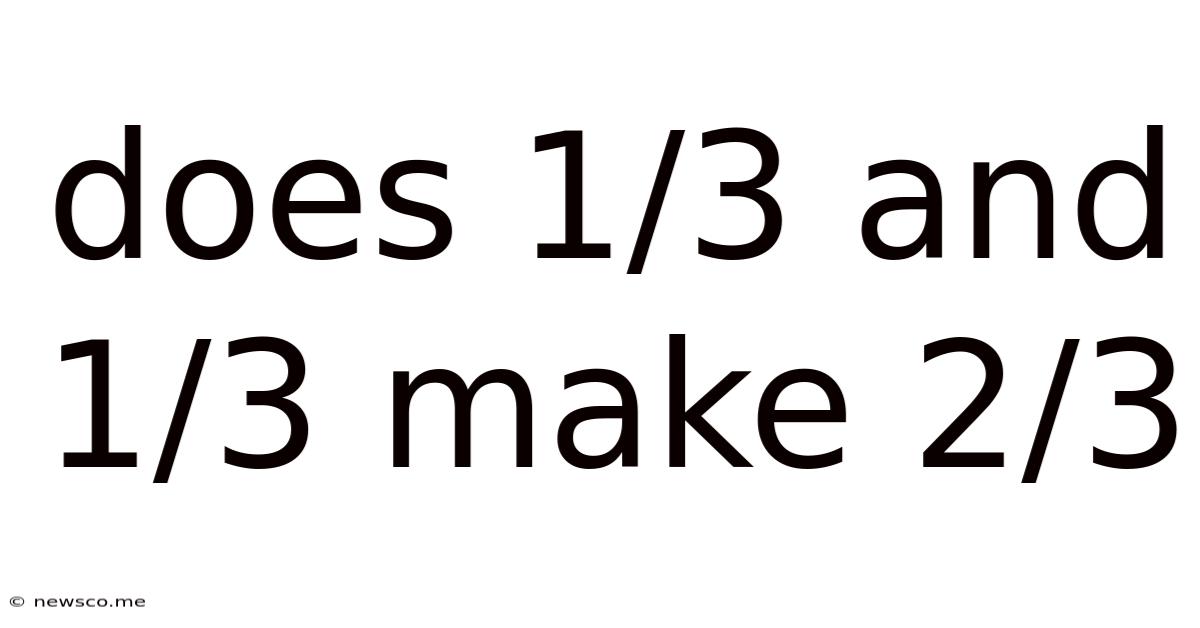
Table of Contents
Does 1/3 + 1/3 = 2/3? A Deep Dive into Fraction Addition
The seemingly simple question, "Does 1/3 + 1/3 = 2/3?" might appear trivial at first glance. However, exploring this question opens a door to a deeper understanding of fractions, their manipulation, and the fundamental principles of arithmetic. This article will not only answer the question definitively but also explore the underlying concepts, providing a comprehensive guide for anyone seeking a firm grasp of fraction addition.
Understanding Fractions: The Building Blocks
Before diving into the addition, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number indicates how many parts we have.
- Denominator: The bottom number indicates how many equal parts the whole is divided into.
For example, in the fraction 1/3, the numerator (1) tells us we have one part, and the denominator (3) tells us the whole is divided into three equal parts.
Adding Fractions with Common Denominators
The key to adding fractions lies in their denominators. When adding fractions with the same denominator (like our 1/3 + 1/3 example), the process is straightforward:
- Add the numerators: Simply add the top numbers. In our case, 1 + 1 = 2.
- Keep the denominator the same: The denominator remains unchanged. It stays as 3.
- Simplify (if necessary): The resulting fraction is 2/3. In this case, it's already in its simplest form.
Therefore, yes, 1/3 + 1/3 = 2/3.
Visualizing the Addition
Visual aids can greatly enhance understanding. Imagine a pizza cut into three equal slices. 1/3 represents one slice. If you add another 1/3 (another slice), you now have 2/3 of the pizza. This visual representation reinforces the mathematical calculation.
Why the Denominator Remains Unchanged
The denominator represents the size of the parts. Since we're adding parts of the same size (both are thirds), the size of the resulting parts doesn't change. We're simply adding the number of parts we possess, not altering their size. This is a crucial concept in understanding fraction addition.
Adding Fractions with Different Denominators
The process becomes slightly more complex when adding fractions with different denominators. In such cases, we need to find a common denominator—a number that is a multiple of both denominators.
Example: Let's add 1/2 + 1/4.
- Find the common denominator: The least common multiple of 2 and 4 is 4.
- Convert fractions to equivalent fractions with the common denominator:
- 1/2 is equivalent to 2/4 (multiply both numerator and denominator by 2).
- Add the numerators: 2/4 + 1/4 = 3/4.
- Keep the denominator the same: The denominator remains 4.
- Simplify (if necessary): 3/4 is already in its simplest form.
Real-World Applications of Fraction Addition
Understanding fraction addition isn't just an academic exercise; it has numerous real-world applications:
- Cooking and Baking: Recipes often involve fractions, and accurately measuring ingredients requires adding fractions. For example, a recipe might call for 1/2 cup of flour and 1/4 cup of sugar.
- Construction and Engineering: Precise measurements are crucial in construction and engineering, and these often involve fractions or decimals (which are closely related to fractions).
- Finance: Calculating percentages, interest rates, and portions of budgets frequently involves fraction addition and manipulation.
- Data Analysis: Understanding data sets, particularly those represented as proportions or percentages, requires a solid understanding of fractions.
Beyond the Basics: More Complex Fraction Problems
While 1/3 + 1/3 = 2/3 is a fundamental example, let's explore more complex scenarios:
Adding more than two fractions: The principle remains the same. If all fractions share a common denominator, simply add the numerators and keep the denominator consistent. If not, find the least common multiple of all denominators and convert all fractions before adding.
Mixed numbers: A mixed number combines a whole number and a fraction (e.g., 1 1/2). To add mixed numbers, add the whole numbers separately and then add the fractions, following the rules described earlier. If the fractional part exceeds 1, simplify it by converting it into a whole number and adding it to the whole number portion.
Subtracting fractions: The process is similar to addition, but you subtract the numerators instead of adding them. Ensure you have a common denominator before subtracting.
Multiplying and dividing fractions: These operations follow different rules than addition and subtraction. Multiplying fractions involves multiplying the numerators together and the denominators together. Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying.
Mastering Fractions: Tips and Tricks
- Practice regularly: The key to mastering fractions is consistent practice. Work through various examples, starting with simple problems and gradually progressing to more complex ones.
- Visual aids: Utilize visual tools like diagrams, charts, or physical objects to reinforce your understanding.
- Seek help when needed: Don't hesitate to ask for help if you're struggling with a particular concept. Teachers, tutors, or online resources can provide valuable support.
- Use online calculators and tools: Numerous online resources offer fraction calculators and interactive learning tools that can aid in your understanding. However, always try to work through problems manually first to solidify your understanding of the underlying principles.
Conclusion: The Importance of Foundational Math
The simple equation, 1/3 + 1/3 = 2/3, serves as a cornerstone for understanding fractions and their manipulation. Mastering fraction addition provides a solid foundation for tackling more complex mathematical concepts and real-world problem-solving. By understanding the underlying principles, visualizing the concepts, and practicing consistently, anyone can confidently navigate the world of fractions and their applications. Remember that a strong grasp of fundamental mathematical concepts is crucial for success in various fields and endeavors. This understanding extends beyond simply knowing the answer; it's about comprehending the why behind the calculation, thereby fostering a deeper appreciation for the beauty and power of mathematics.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Does 1/3 And 1/3 Make 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.