Does 1/4 And 1/4 Equal 1/2
News Co
Apr 12, 2025 · 5 min read
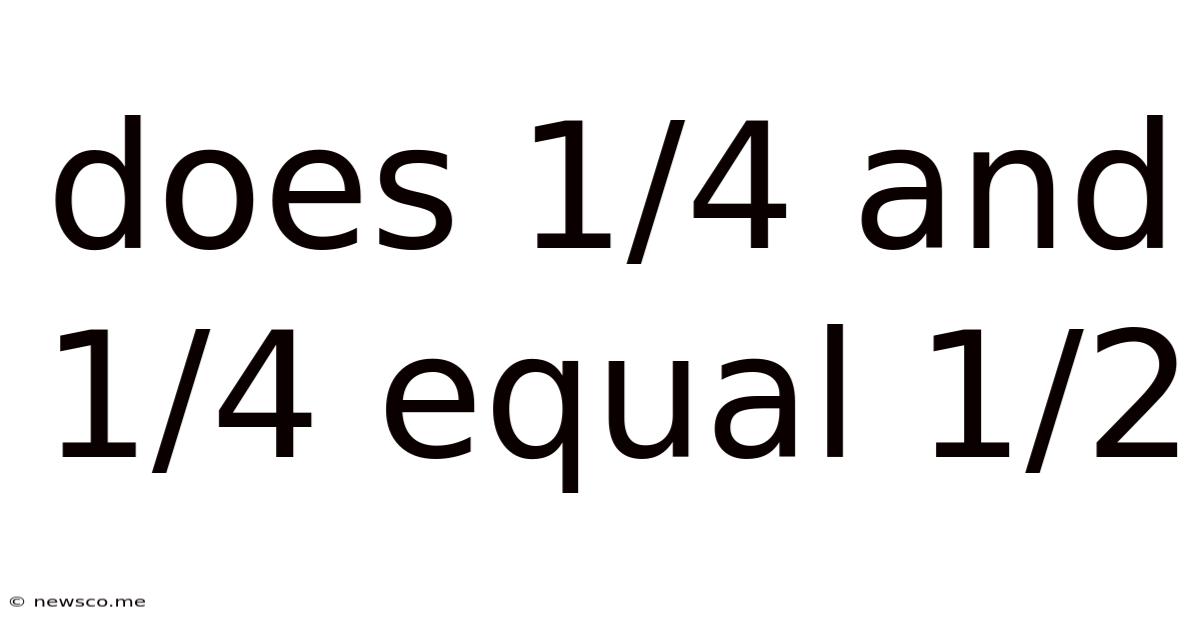
Table of Contents
Does 1/4 + 1/4 Equal 1/2? A Deep Dive into Fraction Addition
The question, "Does 1/4 + 1/4 equal 1/2?" seems deceptively simple. It's a fundamental concept in elementary mathematics, yet understanding the why behind the answer is crucial for building a strong foundation in arithmetic and algebra. This article will not only answer the question definitively but also explore the underlying principles of fraction addition, providing a comprehensive guide for students and anyone looking to refresh their understanding of this essential mathematical operation.
Understanding Fractions: Parts of a Whole
Before diving into the addition itself, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For instance, in the fraction 1/4, the denominator (4) tells us the whole is divided into four equal parts, and the numerator (1) tells us we're considering only one of those parts. Think of a pizza cut into four slices; 1/4 represents one slice.
Adding Fractions: A Step-by-Step Guide
Adding fractions requires a crucial understanding of common denominators. This means that the fractions being added must have the same denominator before you can add their numerators. If the denominators are different, you must find a least common denominator (LCD) before proceeding.
When denominators are the same:
When adding fractions with the same denominator, the process is straightforward:
- Add the numerators: Simply add the numbers in the top of each fraction.
- Keep the denominator the same: The denominator remains unchanged.
- Simplify the result (if necessary): Reduce the fraction to its simplest form by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Let's illustrate with our example:
1/4 + 1/4 = (1 + 1) / 4 = 2/4
Now, we simplify 2/4. Both 2 and 4 are divisible by 2:
2/4 = (2 ÷ 2) / (4 ÷ 2) = 1/2
Therefore, yes, 1/4 + 1/4 = 1/2.
Visual Representation: Making it Concrete
Visual aids can significantly improve understanding, especially with fractions. Imagine two squares, each representing a whole.
- Square 1: Divide it into four equal parts and shade one part. This visually represents 1/4.
- Square 2: Divide it into four equal parts and shade one part. This also represents 1/4.
Now, combine the shaded parts from both squares. You'll see that two out of eight equal parts are shaded, which simplifies to 1/2. This visual demonstration reinforces the mathematical calculation.
Why Common Denominators are Essential
The concept of the common denominator is paramount because fractions represent parts of a whole. You cannot directly add parts of different wholes. Imagine trying to add one quarter of a pizza to one third of a different pizza—you can't simply add the numerators (1+1=2) and the denominators (4+3=7) to get 2/7. That doesn't make logical sense in the context of the whole.
Finding a common denominator ensures you're working with parts of the same whole, making the addition meaningful and accurate.
Adding Fractions with Different Denominators
When the denominators are different, finding the LCD is the first step. The LCD is the smallest number that is a multiple of both denominators.
Let's consider an example: 1/3 + 1/6
-
Find the LCD: The multiples of 3 are 3, 6, 9, 12... The multiples of 6 are 6, 12, 18... The smallest common multiple is 6.
-
Convert fractions to equivalent fractions with the LCD:
- 1/3 is equivalent to 2/6 (multiply numerator and denominator by 2)
-
Add the numerators: 2/6 + 1/6 = (2 + 1) / 6 = 3/6
-
Simplify: 3/6 = 1/2 (both are divisible by 3)
So, 1/3 + 1/6 = 1/2
Real-World Applications: Where Fractions Matter
Understanding fraction addition isn't just an academic exercise; it has numerous real-world applications:
- Cooking and Baking: Recipes often involve fractions of ingredients. Accurately adding fractions ensures the correct proportions are used.
- Construction and Engineering: Precise measurements are vital in these fields. Fractions are frequently used for calculations involving lengths, volumes, and areas.
- Finance: Calculating budgets, interest rates, and shares often involves working with fractions and decimals (which are essentially fractions with denominators that are powers of 10).
- Data Analysis: Representing and analyzing proportions often involves using fractions and percentages.
Beyond the Basics: More Complex Fraction Operations
While this article focuses on the addition of simple fractions, the principles extend to more complex operations:
- Subtracting Fractions: Similar to addition, subtraction requires finding a common denominator before subtracting the numerators.
- Multiplying Fractions: Multiplying fractions involves multiplying the numerators and multiplying the denominators separately. Simplification often follows.
- Dividing Fractions: Dividing by a fraction is the same as multiplying by its reciprocal (flipping the numerator and denominator).
Mastering the basics of fraction addition is the foundation for success in these more advanced operations.
Troubleshooting Common Mistakes
Several common mistakes can occur when adding fractions:
- Forgetting the common denominator: This is the most frequent error. Always ensure fractions have the same denominator before adding the numerators.
- Adding denominators: Remember, only the numerators are added; the denominator remains constant (when it's already common).
- Not simplifying the result: Always reduce the resulting fraction to its simplest form for clarity and accuracy.
Conclusion: Mastering Fractions for Mathematical Proficiency
The seemingly simple question, "Does 1/4 + 1/4 equal 1/2?" opens a door to a deeper understanding of fraction arithmetic. By grasping the concept of common denominators and mastering the step-by-step process of fraction addition, you build a solid foundation for tackling more complex mathematical problems. Remember that visual representations and real-world applications can enhance your comprehension and solidify your understanding of this fundamental mathematical concept. This knowledge is not only crucial for academic success but also invaluable in various aspects of everyday life. So, yes, 1/4 + 1/4 unequivocally equals 1/2, and understanding why is just as important as knowing the answer itself.
Latest Posts
Related Post
Thank you for visiting our website which covers about Does 1/4 And 1/4 Equal 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.