Domain And Range Of All Trig Functions
News Co
Apr 02, 2025 · 6 min read
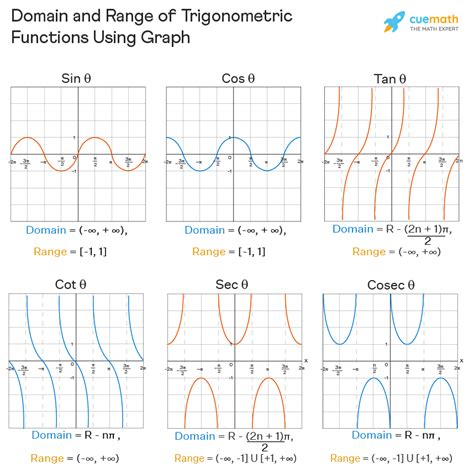
Table of Contents
Domain and Range of Trigonometric Functions: A Comprehensive Guide
Understanding the domain and range of trigonometric functions is crucial for anyone studying mathematics, particularly in calculus, trigonometry, and precalculus. These concepts are fundamental to graphing, solving equations, and applying trigonometric functions in various fields like physics and engineering. This comprehensive guide will delve into the domain and range of all six trigonometric functions—sine, cosine, tangent, cosecant, secant, and cotangent—providing a clear and detailed explanation with examples.
Understanding Domain and Range
Before we dive into the specifics of each trigonometric function, let's establish a clear understanding of what domain and range represent.
-
Domain: The domain of a function is the set of all possible input values (x-values) for which the function is defined. In simpler terms, it's the set of x-values that you can "plug into" the function and get a valid output.
-
Range: The range of a function is the set of all possible output values (y-values) that the function can produce. It's the set of all possible results you can get when you input values from the domain.
The Six Trigonometric Functions: Domain and Range
Let's examine each trigonometric function individually, exploring its domain and range in detail. We'll use the unit circle as a visual aid to understand the behavior of these functions.
1. Sine Function (sin x)
-
Definition: The sine of an angle x is the y-coordinate of the point where the terminal side of the angle intersects the unit circle.
-
Domain: The sine function is defined for all real numbers. You can input any angle (in radians or degrees), and the function will produce a valid output. Therefore, the domain is (-∞, ∞) or all real numbers.
-
Range: The y-coordinate on the unit circle varies between -1 and 1, inclusive. Therefore, the range of the sine function is [-1, 1].
2. Cosine Function (cos x)
-
Definition: The cosine of an angle x is the x-coordinate of the point where the terminal side of the angle intersects the unit circle.
-
Domain: Similar to the sine function, the cosine function is defined for all real numbers. Its domain is (-∞, ∞) or all real numbers.
-
Range: The x-coordinate on the unit circle also varies between -1 and 1, inclusive. Thus, the range of the cosine function is [-1, 1].
3. Tangent Function (tan x)
-
Definition: The tangent of an angle x is defined as the ratio of the sine of x to the cosine of x: tan x = sin x / cos x.
-
Domain: The tangent function is undefined wherever the cosine function is zero. This occurs at odd multiples of π/2 (i.e., ±π/2, ±3π/2, ±5π/2, ...). Therefore, the domain is all real numbers except these points. We can express this as: (-∞, ∞) \ { (2n+1)π/2 | n ∈ Z }, where Z represents the set of integers.
-
Range: The tangent function can take on any real value. As the angle approaches the values where it's undefined, the tangent approaches positive or negative infinity. Thus, the range is (-∞, ∞) or all real numbers.
4. Cosecant Function (csc x)
-
Definition: The cosecant of an angle x is the reciprocal of the sine of x: csc x = 1 / sin x.
-
Domain: The cosecant function is undefined wherever the sine function is zero. This occurs at integer multiples of π (i.e., 0, ±π, ±2π, ...). The domain is all real numbers except these points: (-∞, ∞) \ { nπ | n ∈ Z }.
-
Range: The cosecant function's range is all real numbers greater than or equal to 1 or less than or equal to -1. This can be expressed as (-∞, -1] ∪ [1, ∞).
5. Secant Function (sec x)
-
Definition: The secant of an angle x is the reciprocal of the cosine of x: sec x = 1 / cos x.
-
Domain: The secant function is undefined wherever the cosine function is zero. This occurs at odd multiples of π/2 (i.e., ±π/2, ±3π/2, ±5π/2, ...). The domain is all real numbers except these points: (-∞, ∞) \ { (2n+1)π/2 | n ∈ Z }.
-
Range: Similar to the cosecant, the secant function's range is all real numbers greater than or equal to 1 or less than or equal to -1. This can be expressed as (-∞, -1] ∪ [1, ∞).
6. Cotangent Function (cot x)
-
Definition: The cotangent of an angle x is the reciprocal of the tangent of x: cot x = 1 / tan x = cos x / sin x.
-
Domain: The cotangent function is undefined wherever the sine function is zero. This occurs at integer multiples of π (i.e., 0, ±π, ±2π, ...). The domain is all real numbers except these points: (-∞, ∞) \ { nπ | n ∈ Z }.
-
Range: The cotangent function, like the tangent function, can take on any real value. Its range is (-∞, ∞) or all real numbers.
Visualizing the Domains and Ranges
Using graphing calculators or software can provide a visual representation of these functions, clearly showing their domains and ranges. Observing the asymptotes (vertical lines where the function approaches infinity) will help solidify your understanding of the undefined points in the domain.
Applications and Importance
The understanding of domain and range is crucial for numerous applications:
-
Solving Trigonometric Equations: Knowing the range helps determine if a solution is valid. For example, if an equation results in sin x = 2, you immediately know there is no solution because the sine function's range is [-1, 1].
-
Graphing Trigonometric Functions: Understanding the domain and range allows for accurate sketching of the graphs, identifying asymptotes, and determining the function's behavior.
-
Calculus: Domain and range are essential for finding derivatives, integrals, and limits of trigonometric functions. Understanding where the function is undefined is crucial for analyzing its behavior near those points.
-
Physics and Engineering: Trigonometric functions are extensively used in these fields to model periodic phenomena like oscillations, waves, and rotations. Knowing the domain and range ensures accurate modeling and analysis.
Summary Table
| Function | Domain | Range |
|---|---|---|
| sin x | (-∞, ∞) | [-1, 1] |
| cos x | (-∞, ∞) | [-1, 1] |
| tan x | (-∞, ∞) \ { (2n+1)π/2 | n ∈ Z } |
| csc x | (-∞, ∞) \ { nπ | n ∈ Z } |
| sec x | (-∞, ∞) \ { (2n+1)π/2 | n ∈ Z } |
| cot x | (-∞, ∞) \ { nπ | n ∈ Z } |
This comprehensive guide provides a solid foundation for understanding the domain and range of trigonometric functions. Mastering these concepts is fundamental to success in advanced mathematical studies and their applications in various scientific and engineering fields. Remember to practice regularly and utilize visual aids to strengthen your understanding. Consistent practice will build your confidence and expertise in working with these important mathematical tools.
Latest Posts
Related Post
Thank you for visiting our website which covers about Domain And Range Of All Trig Functions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.