Domains And Ranges Of Trig Functions
News Co
Apr 01, 2025 · 6 min read
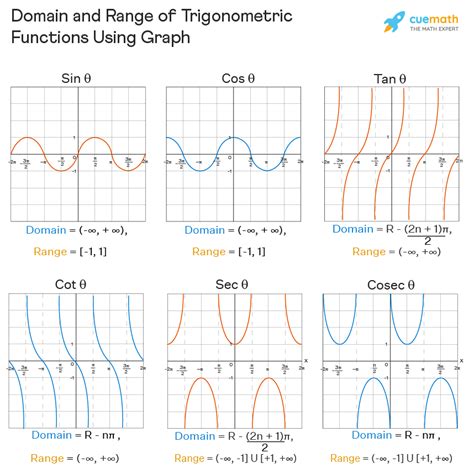
Table of Contents
Domains and Ranges of Trigonometric Functions: A Comprehensive Guide
Trigonometric functions, often shortened to "trig functions," are fundamental building blocks in mathematics, particularly in calculus, geometry, and physics. Understanding their domains and ranges is crucial for correctly applying them and interpreting results. This comprehensive guide will delve deep into the domains and ranges of the six main trigonometric functions: sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot). We'll explore their definitions, visual representations, and practical applications, ensuring a solid grasp of these essential concepts.
Understanding Domains and Ranges
Before diving into the specifics of each trigonometric function, let's clarify the terms "domain" and "range."
-
Domain: The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. In simpler terms, it's all the values you can plug into the function and get a meaningful output.
-
Range: The range of a function is the set of all possible output values (y-values) that the function can produce. It's all the values the function can actually return.
The Six Trigonometric Functions: Domains and Ranges
Let's examine each trigonometric function individually, exploring its domain and range, and illustrating it with both algebraic and graphical representations.
1. Sine (sin x)
-
Definition: The sine of an angle x in a right-angled triangle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse.
-
Domain: The sine function is defined for all real numbers. You can input any angle, whether it's measured in degrees or radians, and the function will produce a meaningful output. Therefore, the domain is (-∞, ∞).
-
Range: The sine function's output always lies between -1 and 1, inclusive. This is because the ratio of the opposite side to the hypotenuse can never exceed 1 (since the hypotenuse is always the longest side). The range is [-1, 1].
-
Graphical Representation: The graph of sin x is a continuous wave oscillating between -1 and 1. It repeats itself every 2π radians (or 360 degrees), demonstrating its periodic nature.
2. Cosine (cos x)
-
Definition: The cosine of an angle x in a right-angled triangle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse.
-
Domain: Similar to the sine function, the cosine function is defined for all real numbers. Its domain is (-∞, ∞).
-
Range: Just like the sine function, the cosine function's output is always between -1 and 1, inclusive. The range is [-1, 1].
-
Graphical Representation: The graph of cos x is also a continuous wave oscillating between -1 and 1, identical in shape to the sine graph but shifted horizontally by π/2 radians (or 90 degrees).
3. Tangent (tan x)
-
Definition: The tangent of an angle x is defined as the ratio of the sine of x to the cosine of x: tan x = sin x / cos x.
-
Domain: The tangent function is undefined whenever the cosine of x is zero. This occurs at odd multiples of π/2 (i.e., π/2, 3π/2, 5π/2, etc.). Therefore, the domain is all real numbers except these points. We can represent this as (-∞, ∞) \ { (2n+1)π/2 | n ∈ Z }, where Z represents the set of integers.
-
Range: The tangent function can take on any real value. As x approaches the values where it's undefined, the function tends towards positive or negative infinity. The range is (-∞, ∞).
-
Graphical Representation: The graph of tan x shows vertical asymptotes at the points where the function is undefined. It's a periodic function with a period of π radians (or 180 degrees).
4. Cosecant (csc x)
-
Definition: The cosecant of an angle x is the reciprocal of the sine of x: csc x = 1 / sin x.
-
Domain: The cosecant function is undefined whenever the sine of x is zero. This occurs at integer multiples of π (i.e., 0, π, 2π, etc.). The domain is all real numbers except these points. We can express this as (-∞, ∞) \ { nπ | n ∈ Z }.
-
Range: The cosecant function's range is all real numbers greater than or equal to 1 or less than or equal to -1. This is because the reciprocal of a number between -1 and 1 will always have an absolute value greater than or equal to 1. The range is (-∞, -1] ∪ [1, ∞).
-
Graphical Representation: The graph of csc x shows vertical asymptotes at the points where the function is undefined. It has a period of 2π radians.
5. Secant (sec x)
-
Definition: The secant of an angle x is the reciprocal of the cosine of x: sec x = 1 / cos x.
-
Domain: The secant function is undefined whenever the cosine of x is zero. This occurs at odd multiples of π/2. The domain is all real numbers except these points: (-∞, ∞) \ { (2n+1)π/2 | n ∈ Z }.
-
Range: Similar to cosecant, the secant function's range is all real numbers greater than or equal to 1 or less than or equal to -1. The range is (-∞, -1] ∪ [1, ∞).
-
Graphical Representation: The graph of sec x has vertical asymptotes at the points where the function is undefined and a period of 2π radians.
6. Cotangent (cot x)
-
Definition: The cotangent of an angle x is the reciprocal of the tangent of x: cot x = 1 / tan x = cos x / sin x.
-
Domain: The cotangent function is undefined whenever the sine of x is zero. This occurs at integer multiples of π. The domain is all real numbers except these points: (-∞, ∞) \ { nπ | n ∈ Z }.
-
Range: The cotangent function can take on any real value. The range is (-∞, ∞).
-
Graphical Representation: The graph of cot x displays vertical asymptotes at the points where it's undefined, and it has a period of π radians.
Applications and Importance of Understanding Domains and Ranges
Knowing the domains and ranges of trigonometric functions is critical for several reasons:
-
Solving Equations: When solving trigonometric equations, understanding the domain helps identify potential solutions and avoid extraneous solutions. The range helps determine if a given equation has any solutions at all.
-
Calculus: In calculus, determining the domain and range is vital for finding derivatives, integrals, and limits of trigonometric functions. Understanding these concepts prevents errors in calculations and interpretations.
-
Graphing: Accurately graphing trigonometric functions requires knowing their domains and ranges to establish the scale and identify asymptotes.
-
Real-World Applications: Trigonometric functions are used extensively in physics, engineering, and other fields to model periodic phenomena like oscillations, waves, and rotations. Understanding their domains and ranges ensures accurate modeling and predictions.
Conclusion
Mastering the domains and ranges of trigonometric functions is a cornerstone of understanding their behavior and applications. By comprehending these fundamental concepts – graphically, algebraically, and conceptually – you can effectively utilize trigonometric functions in various mathematical contexts and real-world problems. This comprehensive guide provides a solid foundation for further exploration into the rich world of trigonometry and its applications. Remember to practice regularly, utilizing different problem-solving approaches to solidify your understanding and improve your proficiency. Consistent practice is key to mastering these essential mathematical concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about Domains And Ranges Of Trig Functions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.