Evaluate The Integral. 7 X2 + 49 Dx 0
News Co
May 07, 2025 · 4 min read
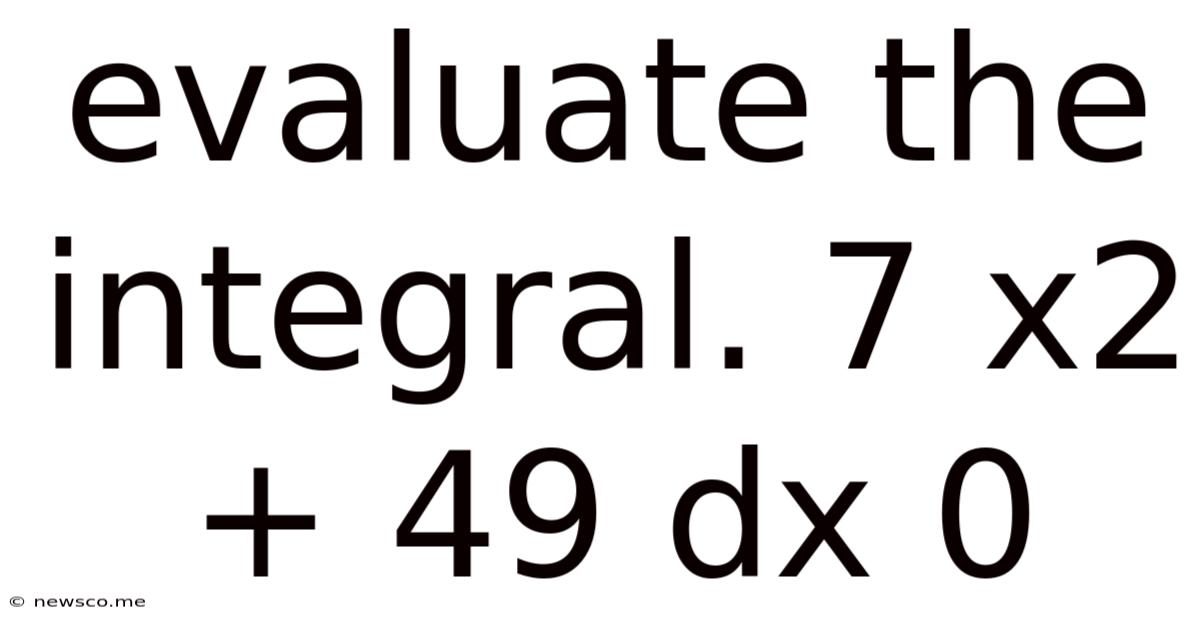
Table of Contents
- Evaluate The Integral. 7 X2 + 49 Dx 0
- Table of Contents
- Evaluating the Definite Integral: ∫₀⁷ (7x² + 49) dx
- Understanding Definite Integrals
- The Fundamental Theorem of Calculus
- Step-by-Step Solution: ∫₀⁷ (7x² + 49) dx
- Practical Applications and Significance
- 1. Area Calculation:**
- 2. Volume Calculation:**
- 3. Probability and Statistics:**
- 4. Physics and Engineering Applications:**
- 5. Financial Modeling:**
- Conclusion: Mastering Definite Integrals
- Latest Posts
- Related Post
Evaluating the Definite Integral: ∫₀⁷ (7x² + 49) dx
Evaluating definite integrals is a fundamental concept in calculus, with wide-ranging applications in various fields like physics, engineering, and economics. This article delves into the step-by-step process of evaluating the definite integral ∫₀⁷ (7x² + 49) dx, providing a comprehensive explanation suitable for students and anyone interested in strengthening their calculus skills. We'll explore the underlying principles, demonstrate the solution method, and discuss potential applications.
Understanding Definite Integrals
A definite integral represents the signed area between a curve and the x-axis over a specified interval. The integral ∫₀⁷ (7x² + 49) dx signifies the area under the curve y = 7x² + 49 from x = 0 to x = 7. The notation itself provides valuable information:
- ∫: This symbol denotes the integration process, essentially finding the antiderivative.
- ₀⁷: These numbers represent the lower and upper limits of integration, defining the interval [0, 7].
- (7x² + 49): This is the integrand, the function whose area under the curve we're calculating.
- dx: This indicates that we are integrating with respect to the variable x.
The Fundamental Theorem of Calculus
The cornerstone of evaluating definite integrals is the Fundamental Theorem of Calculus. This theorem links differentiation and integration, providing a powerful method for calculating definite integrals without resorting to Riemann sums or other limit-based approaches. The theorem states that if F(x) is an antiderivative of f(x), then:
∫ₐᵇ f(x) dx = F(b) - F(a)
This elegantly simplifies the process. We find the antiderivative of the integrand, evaluate it at the upper limit (b), evaluate it at the lower limit (a), and then subtract the two results.
Step-by-Step Solution: ∫₀⁷ (7x² + 49) dx
Let's apply the Fundamental Theorem of Calculus to our problem: ∫₀⁷ (7x² + 49) dx
Step 1: Find the Antiderivative
We need to find the antiderivative of the integrand, 7x² + 49. This involves applying the power rule of integration:
∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C (where n ≠ -1 and C is the constant of integration)
Applying this rule to each term of the integrand:
∫7x² dx = 7 * (x³)/3 + C₁ = (7x³)/3 + C₁
∫49 dx = 49x + C₂
Therefore, the antiderivative of 7x² + 49 is:
F(x) = (7x³)/3 + 49x + C (where C = C₁ + C₂ is the combined constant of integration)
Step 2: Evaluate at the Upper and Lower Limits
Now we evaluate the antiderivative at the upper limit (7) and the lower limit (0):
F(7) = (7(7)³)/3 + 49(7) + C = (7*343)/3 + 343 + C = (2401)/3 + 343 + C
F(0) = (7(0)³)/3 + 49(0) + C = 0 + 0 + C = C
Step 3: Subtract the Results
Finally, we subtract the value of the antiderivative at the lower limit from its value at the upper limit:
∫₀⁷ (7x² + 49) dx = F(7) - F(0) = [(2401)/3 + 343 + C] - C = (2401)/3 + 343
Step 4: Simplify the Result
Now we simplify the expression:
(2401)/3 + 343 = 800.333... + 343 = 1143.333...
Therefore, the definite integral ∫₀⁷ (7x² + 49) dx evaluates to approximately 1143.33. The constant of integration (C) cancels out during the subtraction, as expected.
Practical Applications and Significance
The ability to evaluate definite integrals has far-reaching consequences across various disciplines:
1. Area Calculation:**
As we've seen, the most direct application is calculating the area under a curve. This is crucial in numerous contexts, including:
- Engineering: Determining the area of irregularly shaped cross-sections of structures.
- Physics: Calculating the work done by a variable force.
- Economics: Finding the total consumer or producer surplus in a market.
2. Volume Calculation:**
Definite integrals are also fundamental in computing volumes of solids of revolution. Rotating a curve around an axis generates a solid, and the integral provides the volume.
3. Probability and Statistics:**
In probability and statistics, definite integrals are used to calculate probabilities and expected values for continuous random variables. This is essential for modeling and analyzing various real-world phenomena.
4. Physics and Engineering Applications:**
Definite integrals appear frequently in physics and engineering:
- Calculating displacement from velocity: The integral of velocity with respect to time gives displacement.
- Determining the center of mass: Definite integrals are used to find the centroid of an object.
- Calculating moments of inertia: These integrals are crucial for understanding rotational motion.
5. Financial Modeling:**
In finance, definite integrals are used for:
- Calculating present value of future cash flows: Discounting future payments to their present value.
- Determining bond yields: Calculating the yield to maturity of a bond.
Conclusion: Mastering Definite Integrals
Evaluating definite integrals, as exemplified by our step-by-step solution of ∫₀⁷ (7x² + 49) dx, is a pivotal skill in calculus. Its applications are widespread, impacting various fields. Understanding the Fundamental Theorem of Calculus provides the necessary framework for efficiently and accurately determining the value of these integrals, unlocking their practical significance across diverse applications. Through consistent practice and a strong grasp of the underlying principles, mastering definite integrals becomes a powerful tool for solving complex problems and gaining deeper insights into various quantitative fields. Remember, practice is key! Work through more examples, and you'll quickly develop your proficiency.
Latest Posts
Related Post
Thank you for visiting our website which covers about Evaluate The Integral. 7 X2 + 49 Dx 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.