Express 5 8 As A Percentage
News Co
Apr 21, 2025 · 4 min read
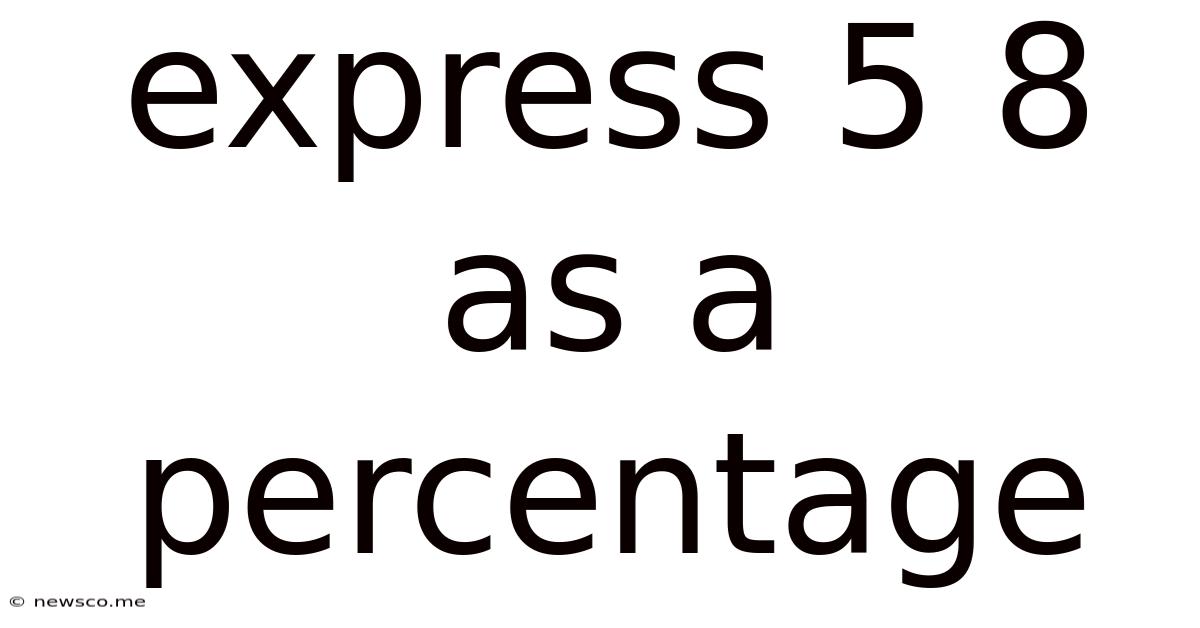
Table of Contents
Expressing 5/8 as a Percentage: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with broad applications in various fields, from finance and statistics to everyday life. This comprehensive guide will delve into the process of expressing 5/8 as a percentage, exploring different methods and providing a deeper understanding of the underlying concepts. We’ll also touch upon practical examples and applications to solidify your grasp of this crucial concept.
Understanding Fractions and Percentages
Before diving into the conversion, let's refresh our understanding of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into. In our case, 5/8 means we have 5 parts out of a total of 8 equal parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per hundred" or "out of 100". For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: Converting the Fraction to a Decimal, Then to a Percentage
This is arguably the most common and straightforward method. It involves two steps:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, we divide the numerator by the denominator:
5 ÷ 8 = 0.625
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.625 × 100 = 62.5%
Therefore, 5/8 is equal to 62.5%.
Method 2: Using Equivalent Fractions
This method involves finding an equivalent fraction with a denominator of 100. While this method might not always be practical for all fractions, it offers a valuable understanding of the relationship between fractions and percentages.
To find an equivalent fraction with a denominator of 100, we need to find a number that, when multiplied by 8, gives us 100. Unfortunately, there isn't a whole number that satisfies this condition. However, we can still use this concept to illustrate the principle.
If we had a fraction like 25/100, we could directly say this is 25%. In the case of 5/8, we could attempt to find a close approximation. This method becomes less efficient and more prone to approximation errors compared to the decimal conversion method.
Method 3: Proportional Reasoning
This approach uses the concept of proportion to solve the problem. We set up a proportion:
5/8 = x/100
Where 'x' represents the percentage we're looking for. To solve for 'x', we cross-multiply:
8x = 500
x = 500 ÷ 8
x = 62.5
Therefore, 5/8 is equal to 62.5%. This method is mathematically equivalent to the first method but highlights the proportional relationship between the fraction and the percentage.
Practical Applications and Examples
The conversion of fractions to percentages is frequently used in various real-world scenarios. Here are some examples:
-
Calculating Discounts: A store offers a 5/8 discount on an item. To determine the discount percentage, we convert 5/8 to 62.5%, meaning the item is discounted by 62.5%.
-
Financial Calculations: In finance, percentages are crucial for calculating interest rates, profits, and losses. If you receive 5/8 of your investment back as profit, this represents a 62.5% return on investment.
-
Statistical Analysis: Percentages are widely used to represent data in statistics and surveys. If 5 out of 8 students in a class passed an exam, this represents a 62.5% pass rate.
-
Everyday Life: Percentages are used in daily life for various tasks, such as calculating tips, understanding sales tax, and comparing prices.
Advanced Concepts and Considerations
While converting 5/8 to a percentage is relatively straightforward, it’s important to consider the following:
-
Rounding: In some cases, the resulting percentage might not be a whole number. You may need to round the percentage to a specific number of decimal places depending on the context. For instance, in financial contexts, precision is crucial, while in some casual settings, rounding to the nearest whole number might suffice.
-
Dealing with Complex Fractions: For more complex fractions, the decimal conversion method remains the most efficient approach. However, understanding the underlying principles remains crucial for solving more complex percentage problems.
Conclusion: Mastering Percentage Conversions
Expressing 5/8 as a percentage, resulting in 62.5%, is a fundamental mathematical skill with wide-ranging applications. Understanding the different methods—converting to decimals, using equivalent fractions (although less practical in this specific case), and proportional reasoning—provides a solid foundation for tackling various percentage problems. Remember to consider rounding and the context of the problem when dealing with percentage calculations. Mastering this skill empowers you to confidently approach diverse scenarios in academics, finance, and daily life, enhancing your numerical literacy and problem-solving abilities. By understanding the underlying principles, you can confidently tackle more complex percentage problems in the future. Keep practicing, and you'll soon become proficient in these essential calculations!
Latest Posts
Related Post
Thank you for visiting our website which covers about Express 5 8 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.