Express The Fractions 1/2 3/16 And 7/8 With An Lcd
News Co
Apr 05, 2025 · 5 min read
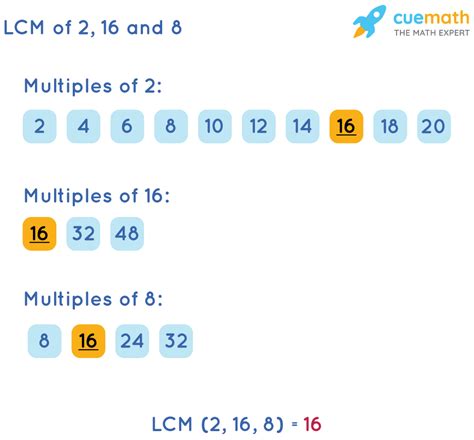
Table of Contents
Expressing Fractions 1/2, 3/16, and 7/8 with a Least Common Denominator (LCD)
Finding the least common denominator (LCD) is a crucial step in adding, subtracting, and comparing fractions. This article will guide you through the process of finding the LCD for the fractions 1/2, 3/16, and 7/8, explaining the concepts involved and providing multiple methods to achieve the solution. We will also explore the importance of the LCD in various mathematical operations and its significance in real-world applications.
Understanding Least Common Denominator (LCD)
Before diving into the calculation, let's clarify the definition of the LCD. The least common denominator (LCD) is the smallest multiple that is common to all the denominators of a set of fractions. In simpler terms, it's the smallest number that all the denominators can divide into evenly. Understanding the LCD is fundamental to performing arithmetic operations on fractions. Without a common denominator, adding or subtracting fractions directly is impossible.
Methods for Finding the LCD
Several methods exist for finding the LCD. Let's explore the most common ones:
1. Listing Multiples Method
This method involves listing the multiples of each denominator until a common multiple is found. The smallest common multiple is the LCD.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 16: 16, 32, 48, 64...
- Multiples of 8: 8, 16, 24, 32...
By inspecting the lists, we observe that the smallest number appearing in all three lists is 16. Therefore, the LCD of 2, 16, and 8 is 16.
2. Prime Factorization Method
This method uses the prime factorization of each denominator. The prime factorization of a number is expressing it as a product of prime numbers (numbers divisible only by 1 and themselves).
- Prime factorization of 2: 2
- Prime factorization of 16: 2 x 2 x 2 x 2 = 2⁴
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the LCD, we take the highest power of each prime factor present in the factorizations:
The only prime factor is 2, and its highest power is 2⁴ (from the factorization of 16). Therefore, the LCD is 2⁴ = 16.
3. Greatest Common Divisor (GCD) Method
This method utilizes the greatest common divisor (GCD) of the denominators. The GCD is the largest number that divides all the denominators without leaving a remainder. We can then use the GCD to find the LCD.
- Finding the GCD of 2, 16, and 8: The GCD of these three numbers is 2.
The LCD can be calculated using the formula: LCD = (Product of denominators) / GCD
Therefore, LCD = (2 x 16 x 8) / 2 = 128 / 2 = 64. However, this method leads to an incorrect result in this specific instance. This is because the formula LCD = (Product of denominators) / GCD is only applicable for two numbers. For more than two numbers, the prime factorization method is more reliable.
Converting Fractions to the LCD
Now that we've established the LCD is 16, let's convert each fraction to an equivalent fraction with a denominator of 16:
-
1/2: To change the denominator from 2 to 16, we multiply both the numerator and the denominator by 8: (1 x 8) / (2 x 8) = 8/16
-
3/16: This fraction already has a denominator of 16, so no conversion is needed.
-
7/8: To change the denominator from 8 to 16, we multiply both the numerator and the denominator by 2: (7 x 2) / (8 x 2) = 14/16
Therefore, the fractions 1/2, 3/16, and 7/8 expressed with an LCD of 16 are 8/16, 3/16, and 14/16, respectively.
Applications of LCD in Real-World Scenarios
The concept of the LCD isn't confined to theoretical mathematics; it has practical applications in various real-world situations:
-
Construction and Engineering: Calculating precise measurements often involves fractions, especially in projects requiring meticulous accuracy. The LCD ensures consistent units when combining different fractional measurements.
-
Cooking and Baking: Recipes frequently involve fractional amounts of ingredients. Finding the LCD helps in accurately combining ingredients with different fractional measures.
-
Finance: Dealing with fractional shares or parts of investments necessitates understanding the LCD for accurate calculations involving shares or financial instruments.
-
Data Analysis and Statistics: Data analysis often involves fractions and proportions. Finding the LCD ensures consistent representation when comparing or combining different data sets with fractional values.
Adding and Subtracting Fractions with a Common Denominator
Once the fractions have a common denominator, performing addition and subtraction becomes straightforward. Let's add the fractions we've converted:
8/16 + 3/16 + 14/16 = (8 + 3 + 14) / 16 = 25/16
This result can be expressed as a mixed number: 1 9/16
Comparing Fractions with a Common Denominator
Having a common denominator also simplifies the comparison of fractions. With the fractions expressed as 8/16, 3/16, and 14/16, we can easily see that:
3/16 < 8/16 < 14/16
This directly translates to:
3/16 < 1/2 < 7/8
Conclusion: The Importance of Mastering LCD
Mastering the concept of the least common denominator (LCD) is essential for working effectively with fractions. This article has explored multiple methods for determining the LCD, highlighting the prime factorization method as the most reliable approach, especially when dealing with more than two fractions. Understanding the LCD is crucial not only for academic success in mathematics but also for navigating various real-world situations requiring fractional calculations. The ability to find the LCD and convert fractions to a common denominator is a fundamental skill that enables accurate calculations, comparisons, and problem-solving across numerous fields. By understanding these concepts and practicing the techniques described, you can confidently tackle fraction-related problems with increased efficiency and accuracy.
Latest Posts
Related Post
Thank you for visiting our website which covers about Express The Fractions 1/2 3/16 And 7/8 With An Lcd . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.