Factor Of X 2 5x 6
News Co
Mar 23, 2025 · 5 min read
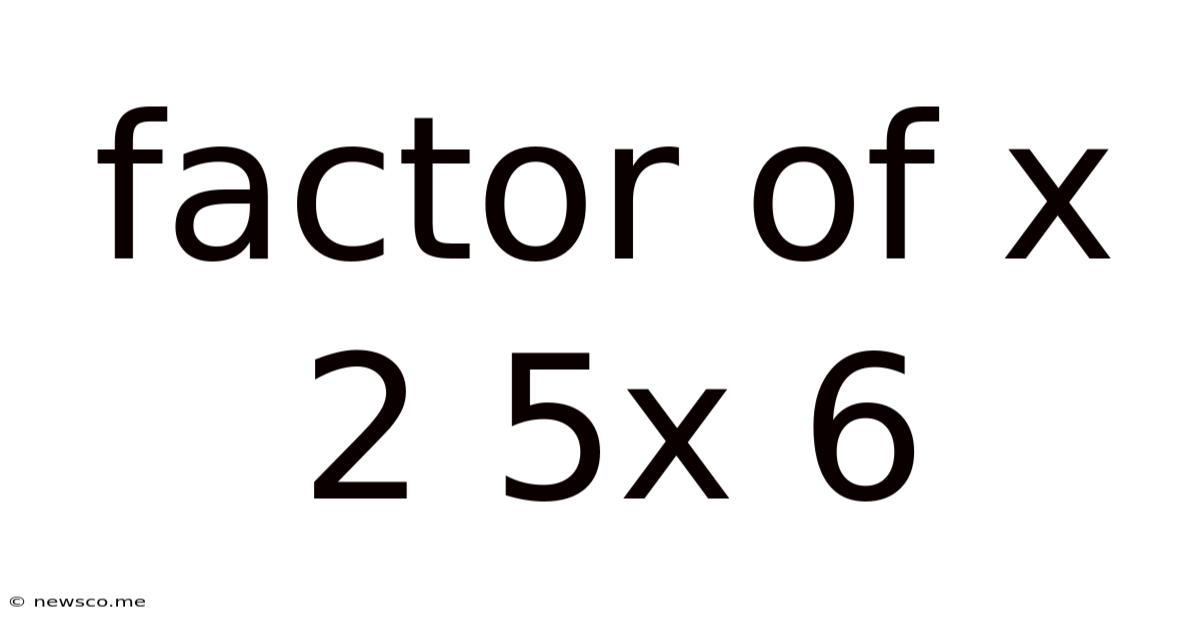
Table of Contents
Factoring the Quadratic Expression: x² + 5x + 6
Factoring quadratic expressions is a fundamental skill in algebra, crucial for solving quadratic equations, simplifying rational expressions, and understanding the behavior of parabolic functions. This article delves deep into the process of factoring the specific quadratic expression x² + 5x + 6, exploring various methods, and illustrating the underlying principles. We'll also touch upon the broader context of factoring quadratics and their applications.
Understanding Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. It generally takes the form ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Our focus is on x² + 5x + 6, where a = 1, b = 5, and c = 6.
The Goal of Factoring
Factoring a quadratic expression involves rewriting it as a product of two simpler expressions, usually two binomials. This process reverses the expansion of binomials using the distributive property (also known as FOIL). The factored form helps in solving equations, simplifying expressions, and revealing important characteristics of the quadratic function represented by the expression.
Method 1: Finding Factors of 'c' that Add Up to 'b'
This is the most common and often the quickest method for factoring simple quadratics like x² + 5x + 6, where the coefficient of x² (a) is 1.
Steps:
-
Identify 'b' and 'c': In our expression, b = 5 and c = 6.
-
Find pairs of factors of 'c': We need to find pairs of numbers that multiply to 6. These pairs are (1, 6), (2, 3), (-1, -6), and (-2, -3).
-
Check which pair adds up to 'b': We look for the pair that adds up to 5. The pair (2, 3) satisfies this condition (2 + 3 = 5).
-
Write the factored form: The factored form is (x + 2)(x + 3).
Verification:
We can verify our answer by expanding the factored form using the FOIL method (First, Outer, Inner, Last):
(x + 2)(x + 3) = x² + 3x + 2x + 6 = x² + 5x + 6
This matches our original expression, confirming that (x + 2)(x + 3) is the correct factorization.
Method 2: The AC Method (for quadratics where a ≠ 1)
While our example has a = 1, the AC method is a valuable technique for factoring quadratics where the coefficient of x² is not 1. Let's illustrate with a slightly more complex example before applying the concept to our original problem.
Consider the quadratic 2x² + 7x + 3.
Steps:
-
Multiply 'a' and 'c': a * c = 2 * 3 = 6
-
Find factors of 'ac' that add up to 'b': We need factors of 6 that add up to 7. The pair (6, 1) fits the bill.
-
Rewrite the middle term: Rewrite 7x as 6x + 1x: 2x² + 6x + 1x + 3
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
2x(x + 3) + 1(x + 3)
-
Factor out the common binomial: (x + 3) is common to both terms, so we factor it out: (x + 3)(2x + 1)
This is the factored form of 2x² + 7x + 3. The AC method is more general and applicable even when the coefficient of x² is 1, although the simpler method 1 is generally preferred in that case.
Applying the AC method to x² + 5x + 6 (even though it's unnecessary in this case) would yield the same result:
- a * c = 1 * 6 = 6
- Factors of 6 that add up to 5 are 2 and 3.
- Rewrite: x² + 2x + 3x + 6
- Factor by grouping: x(x + 2) + 3(x + 2)
- Factored form: (x + 2)(x + 3)
Method 3: Using the Quadratic Formula (for finding roots)
The quadratic formula is a powerful tool for finding the roots (or solutions) of a quadratic equation, which are the values of x that make the quadratic expression equal to zero. While not directly factoring, the roots can be used to determine the factored form.
The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
For x² + 5x + 6, a = 1, b = 5, and c = 6. Plugging these values into the formula gives:
x = [-5 ± √(5² - 4 * 1 * 6)] / 2 * 1 = [-5 ± √1] / 2
This yields two roots: x = -2 and x = -3.
Since the roots are -2 and -3, the factored form is (x + 2)(x + 3). This is because if we set the expression equal to zero, (x+2)(x+3) = 0, the solutions (roots) are x = -2 and x = -3.
Applications of Factoring Quadratic Expressions
Factoring quadratic expressions has numerous applications in various areas of mathematics and beyond:
-
Solving Quadratic Equations: Setting the quadratic expression equal to zero and factoring allows us to easily solve for the values of x.
-
Simplifying Rational Expressions: Factoring the numerator and denominator of a rational expression often leads to simplification by canceling common factors.
-
Graphing Quadratic Functions: The factored form helps identify the x-intercepts (where the parabola crosses the x-axis) of the graph of the quadratic function.
-
Calculus: Factoring plays a significant role in calculus, especially in finding derivatives and integrals.
-
Physics and Engineering: Quadratic equations model many physical phenomena, and factoring helps analyze these models. For example, projectile motion and the path of a ball can be modeled using quadratic equations.
Conclusion: Mastering Quadratic Factoring
Factoring the quadratic expression x² + 5x + 6 is a straightforward process once you understand the underlying principles. Whether you use the method of finding factors of 'c' that add up to 'b', the AC method, or even the quadratic formula indirectly, the result remains the same: (x + 2)(x + 3). Mastering these techniques is essential for success in algebra and related fields, providing a solid foundation for tackling more complex mathematical problems. Remember to practice regularly to build your proficiency and confidence in factoring quadratic expressions. The more you practice, the faster and more intuitively you'll be able to factor these expressions. This will not only help you in your academic pursuits but also enhance your problem-solving skills in various contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about Factor Of X 2 5x 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.