Factors Of -36 That Add Up To -5
News Co
May 08, 2025 · 4 min read
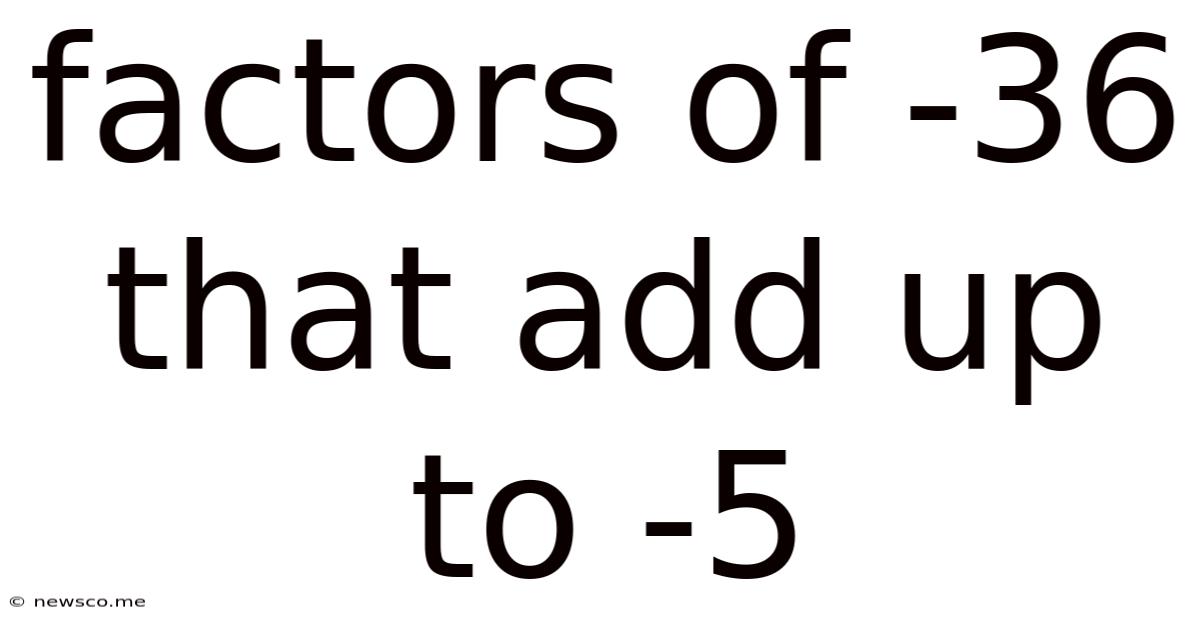
Table of Contents
Factors of -36 That Add Up to -5: A Deep Dive into Number Theory
Finding factors of a number and understanding their relationships is a fundamental concept in number theory. This article delves into the specific problem of identifying the factors of -36 that, when added together, result in a sum of -5. We'll explore different approaches to solving this problem, discuss the underlying mathematical principles, and highlight the practical applications of such number theory concepts.
Understanding Factors and Their Properties
Before diving into the problem, let's establish a firm grasp of what factors are. Factors of a number are whole numbers that divide the number evenly without leaving a remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. Because we're dealing with -36, we must consider both positive and negative factors, as a negative number multiplied by a positive number results in a negative number.
This means the factors of -36 include: ±1, ±2, ±3, ±4, ±6, ±9, ±12, ±18, and ±36. Notice the inclusion of both positive and negative counterparts for each factor. This is crucial for finding the pair that satisfies our sum condition.
Systematic Approaches to Finding the Solution
Several methods can be employed to identify the pair of factors of -36 that add up to -5. Let's explore two prominent approaches:
1. The Exhaustive Search Method
This method involves systematically examining all possible pairs of factors of -36. While straightforward, it can become time-consuming for larger numbers. Let's list the pairs and their sums:
- (1, -36): Sum = -35
- (2, -18): Sum = -16
- (3, -12): Sum = -9
- (4, -9): Sum = -5 <- This is our solution!
- (6, -6): Sum = 0
- (-1, 36): Sum = 35
- (-2, 18): Sum = 16
- (-3, 12): Sum = 9
- (-4, 9): Sum = 5
- (-6, 6): Sum = 0
As we can see, the pair (4, -9) is the only combination that fulfills the condition of adding up to -5.
2. The Algebraic Approach
A more sophisticated approach involves setting up an algebraic equation. Let's represent the two factors as 'x' and 'y'. We know that:
- x * y = -36 (The product of the factors is -36)
- x + y = -5 (The sum of the factors is -5)
We can solve this system of equations using substitution or elimination. Let's use substitution:
From the second equation, we can express y as: y = -5 - x
Substitute this expression for 'y' into the first equation:
x * (-5 - x) = -36
Expanding this equation, we get a quadratic equation:
-5x - x² = -36
Rearrange the equation to the standard quadratic form:
x² + 5x - 36 = 0
Now, we can factor this quadratic equation:
(x + 9)(x - 4) = 0
This gives us two possible solutions for x:
- x = -9
- x = 4
If x = -9, then y = -5 - (-9) = 4. If x = 4, then y = -5 - 4 = -9. Both solutions yield the same factor pair: (4, -9).
Significance and Applications
This seemingly simple problem of finding factors of -36 that add up to -5 has significant implications in various mathematical and practical applications:
1. Quadratic Equations and Factoring
As demonstrated in the algebraic approach, this problem directly relates to solving quadratic equations. The ability to factor quadratic expressions is essential in many areas of mathematics, including calculus, physics, and engineering.
2. Polynomial Factorization
The concept extends beyond quadratic equations. Finding factors that add up to a specific value is crucial in factoring higher-degree polynomials. This has applications in advanced algebra and computer science.
3. Cryptography
Number theory, including factorization, forms the basis of many modern cryptographic systems. The difficulty of factoring large numbers is used to secure sensitive information.
4. Combinatorics and Probability
In combinatorics and probability, understanding the factors of a number and their relationships can be helpful in calculating combinations and permutations.
5. Optimization Problems
In various optimization problems, finding the right factors can lead to efficient solutions. For example, in resource allocation, determining the optimal distribution may involve finding factors of a total resource amount that meet specific constraints.
Expanding the Concept: Generalizing the Problem
The problem we addressed can be generalized to finding factors of any integer 'n' that add up to a given integer 's'. The methods we discussed – exhaustive search and the algebraic approach – can be applied to solve such generalized problems. The algebraic approach typically leads to a quadratic equation (or a higher-degree polynomial equation for more complex cases) that needs to be solved.
Conclusion: From Simple Factors to Complex Applications
While finding the factors of -36 that add up to -5 might seem like a straightforward exercise, it reveals a deeper connection to fundamental concepts in number theory and their extensive applications in various fields. Mastering the techniques for solving such problems, whether through exhaustive search or algebraic methods, lays a solid foundation for understanding more complex mathematical ideas and problem-solving strategies. The ability to identify and manipulate factors, and their sums and products, is a building block for success in numerous areas of study and practice. This problem highlights the interconnectedness of seemingly disparate mathematical concepts and their pervasive impact across multiple disciplines.
Latest Posts
Related Post
Thank you for visiting our website which covers about Factors Of -36 That Add Up To -5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.