Figure Abcd Is A Parallelogram.what Is The Value Of X
News Co
Apr 06, 2025 · 5 min read
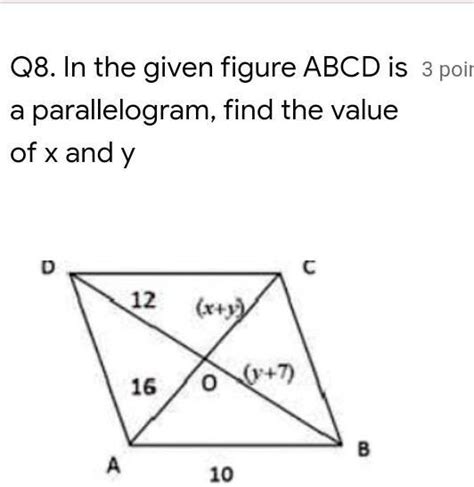
Table of Contents
Figure ABCD is a Parallelogram: What is the Value of x? A Comprehensive Guide
Finding the value of 'x' in a parallelogram problem might seem straightforward, but the approach varies dramatically depending on the given information. This comprehensive guide will explore various scenarios, providing step-by-step solutions and helpful tips to master these geometry problems. We'll delve into different parallelogram properties and how they relate to solving for 'x', equipping you with the skills to tackle any similar problem confidently.
Understanding Parallelograms and Their Properties
Before we jump into solving for 'x', let's refresh our understanding of parallelograms and their key properties:
- Opposite sides are parallel and equal in length: This is the defining characteristic of a parallelogram. Sides AB and CD are parallel and equal, as are sides BC and AD.
- Opposite angles are equal: ∠A = ∠C and ∠B = ∠D.
- Consecutive angles are supplementary: This means that the sum of any two adjacent angles is 180°. For example, ∠A + ∠B = 180°.
- Diagonals bisect each other: The diagonals AC and BD intersect at a point (let's call it E) where AE = EC and BE = ED.
These properties are crucial for solving for 'x' in various parallelogram problems. The specific property you'll use depends entirely on the information provided in the diagram.
Scenario 1: Solving for x using Opposite Sides
Let's assume we have a parallelogram ABCD where AB = 2x + 5, and CD = 3x - 2. Since opposite sides of a parallelogram are equal, we can set up an equation:
2x + 5 = 3x - 2
Solving for x:
Subtract 2x from both sides: 5 = x - 2
Add 2 to both sides: x = 7
Therefore, the value of x is 7.
Example:
Imagine a parallelogram with AB labeled as (2x + 5) cm and CD labeled as (3x - 2) cm. By using the property that opposite sides are equal, we establish the equation 2x + 5 = 3x - 2. Solving this equation yields x = 7. This means that AB = 2(7) + 5 = 19 cm, and CD = 3(7) - 2 = 19 cm, confirming the equality of opposite sides.
Scenario 2: Solving for x using Opposite Angles
Suppose we're given a parallelogram with ∠A = 4x + 10° and ∠C = 6x - 20°. Since opposite angles are equal, we set up the equation:
4x + 10 = 6x - 20
Solving for x:
Subtract 4x from both sides: 10 = 2x - 20
Add 20 to both sides: 30 = 2x
Divide both sides by 2: x = 15
Thus, the value of x is 15. You can check your answer by substituting x = 15 back into the angle expressions. ∠A = 4(15) + 10 = 70°, and ∠C = 6(15) - 20 = 70°, confirming that the opposite angles are equal.
Example:
In parallelogram ABCD, angle A is expressed as (4x + 10)° and angle C as (6x - 20)°. Using the property of equal opposite angles, the equation 4x + 10 = 6x - 20 is formed. Solving this leads to x = 15. Substituting this value back into the angle expressions verifies that both angles A and C equal 70°.
Scenario 3: Solving for x using Consecutive Angles
Consider a parallelogram where ∠A = 3x + 25° and ∠B = 2x + 35°. Remember that consecutive angles are supplementary, meaning their sum is 180°. Therefore:
3x + 25 + 2x + 35 = 180
Combining like terms: 5x + 60 = 180
Subtract 60 from both sides: 5x = 120
Divide both sides by 5: x = 24
Hence, the value of x is 24. To verify, substitute x = 24 into the angle expressions: ∠A = 3(24) + 25 = 97°, and ∠B = 2(24) + 35 = 83°. Notice that 97° + 83° = 180°, confirming the supplementary nature of consecutive angles.
Example:
Given consecutive angles in parallelogram ABCD, angle A is represented as (3x + 25)° and angle B as (2x + 35)°. Their sum must equal 180°, leading to the equation 3x + 25 + 2x + 35 = 180. Solving for x gives x = 24. Substituting x back confirms that angle A is 97° and angle B is 83°, which add up to 180°.
Scenario 4: Solving for x using Diagonals
If the diagonals of parallelogram ABCD intersect at point E, and we are given that AE = 2x + 3 and EC = 3x - 7, we can use the property that diagonals bisect each other. This means AE = EC, so we have:
2x + 3 = 3x - 7
Solving for x:
Subtract 2x from both sides: 3 = x - 7
Add 7 to both sides: x = 10
Therefore, the value of x is 10. Substituting x = 10 into the expressions gives AE = 2(10) + 3 = 23 and EC = 3(10) - 7 = 23, verifying the equal lengths of the bisected diagonal segments.
Example:
In parallelogram ABCD, the diagonals intersect at E. Given that AE = (2x + 3) units and EC = (3x - 7) units, we utilize the diagonal bisecting property to create the equation 2x + 3 = 3x - 7. Solving for x, we obtain x = 10. Substituting this into the expressions for AE and EC confirms that both segments measure 23 units.
Advanced Scenarios and Problem-Solving Strategies
The examples above represent common scenarios. However, more complex problems might involve:
- Combining multiple properties: You might need to use a combination of properties (e.g., opposite sides and consecutive angles) to solve for 'x'.
- Using trigonometry: Some problems may involve angles and require trigonometric functions (sine, cosine, tangent) to find 'x'.
- Algebraic manipulation: More intricate algebraic manipulation might be necessary to isolate 'x' in the equation.
General Problem-Solving Strategies:
- Identify the given information: Carefully examine the diagram and note down all the given values and labels.
- Identify the relevant properties: Determine which parallelogram properties are applicable based on the given information.
- Formulate equations: Create equations based on the chosen properties, linking the given values and the unknown 'x'.
- Solve the equations: Use algebraic techniques to solve for 'x'.
- Verify your answer: Substitute the calculated value of 'x' back into the original equations and expressions to ensure consistency and accuracy. Check if the calculated values make logical sense within the context of parallelogram properties.
Conclusion
Mastering parallelogram problems, particularly solving for 'x', requires a solid understanding of parallelogram properties and adept algebraic manipulation skills. By systematically applying the strategies outlined in this guide, you'll gain confidence in tackling a wide range of parallelogram geometry problems. Remember to always double-check your work to ensure accuracy and to thoroughly understand the underlying geometric principles. With practice, you'll become proficient in solving for 'x' in any parallelogram scenario.
Latest Posts
Related Post
Thank you for visiting our website which covers about Figure Abcd Is A Parallelogram.what Is The Value Of X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.