Find Ac If Ab 16 And Bc 12
News Co
May 08, 2025 · 4 min read
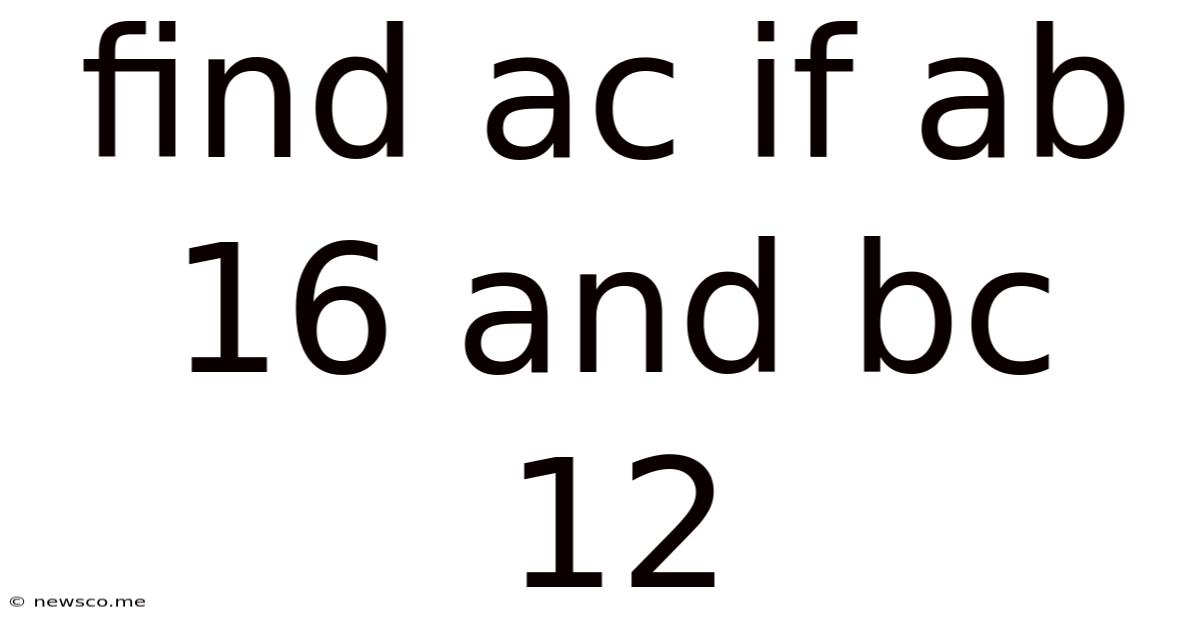
Table of Contents
Finding AC: Exploring the Possibilities When AB = 16 and BC = 12
This article delves into the problem of determining the length of side AC given that AB = 16 and BC = 12. This seemingly simple geometry problem opens up a fascinating exploration of different geometric shapes and the application of various theorems. We will examine different scenarios, illustrating how the solution changes depending on the relationship between points A, B, and C.
Scenario 1: A, B, and C are Collinear
The simplest scenario is when points A, B, and C lie on a straight line. In this case, there are two possibilities:
Possibility 1.1: B is between A and C
If B lies between A and C, then AC is simply the sum of AB and BC.
AC = AB + BC = 16 + 12 = 28
This is a straightforward application of the segment addition postulate.
Possibility 1.2: A is between B and C
If A lies between B and C, then AC is the difference between BC and AB.
AC = BC - AB = 12 - 16 = -4
Since length cannot be negative, this scenario is impossible given the provided values for AB and BC.
Scenario 2: A, B, and C form a Triangle
If A, B, and C are not collinear, they form a triangle. The length of AC depends on the angle at B. To find AC, we need more information, specifically the angle ∠ABC.
The Triangle Inequality Theorem
Before exploring different angles, let's consider the Triangle Inequality Theorem. This theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. In our case:
- AB + BC > AC
- AB + AC > BC
- BC + AC > AB
Substituting the known values:
- 16 + 12 > AC => 28 > AC
- 16 + AC > 12 => AC > -4 (always true since AC must be positive)
- 12 + AC > 16 => AC > 4
Combining these inequalities, we get: 4 < AC < 28
This establishes a range of possible values for AC. The exact value depends on the angle at B (∠ABC).
Using the Law of Cosines
The Law of Cosines provides a powerful tool for finding the length of a side of a triangle when we know the lengths of the other two sides and the angle between them. The formula is:
c² = a² + b² - 2ab cos(C)
Where:
- a and b are the lengths of two sides of the triangle
- C is the angle between sides a and b
- c is the length of the side opposite angle C
In our case, let:
- a = AB = 16
- b = BC = 12
- c = AC
- C = ∠ABC
Therefore, the Law of Cosines becomes:
AC² = 16² + 12² - 2 * 16 * 12 * cos(∠ABC)
AC² = 256 + 144 - 384 * cos(∠ABC)
AC² = 400 - 384 * cos(∠ABC)
We can see that the length of AC is directly dependent on the value of ∠ABC.
- If ∠ABC = 0° (collinear, B between A and C): cos(0°) = 1, AC² = 400 - 384 = 16, AC = 4 (This contradicts the previously calculated 28, highlighting the importance of specifying the arrangement of the points).
- If ∠ABC = 180° (collinear, A between B and C): cos(180°) = -1, AC² = 400 + 384 = 784, AC = 28 (This aligns with our earlier calculation for this collinear arrangement).
- If ∠ABC = 90° (right-angled triangle): cos(90°) = 0, AC² = 400, AC = 20. This is a Pythagorean triple (12, 16, 20).
For any other angle between 0° and 180°, the value of AC will fall within the range 4 < AC < 28.
Scenario 3: Advanced Considerations
The problem becomes even more complex if we consider higher dimensions or non-Euclidean geometries. However, within the context of standard Euclidean geometry, the key takeaway is the dependence of AC on the angle ∠ABC.
Practical Applications
Understanding this problem has practical applications in various fields:
- Surveying: Determining distances between points using triangulation.
- Construction: Calculating the dimensions of structures.
- Navigation: Estimating distances based on known coordinates.
- Computer Graphics: Calculating distances and positions in 2D and 3D spaces.
Conclusion: The Importance of Context
The question of finding AC when AB = 16 and BC = 12 highlights the crucial role of context in mathematical problems. Without additional information, particularly the relationship between points A, B, and C (collinear or forming a triangle, and if a triangle, the angle at B), a definitive answer is impossible. This exploration showcases the power of geometric theorems, like the Triangle Inequality Theorem and the Law of Cosines, in solving seemingly simple geometric problems. Understanding the limitations and possibilities inherent in these problems is essential for applying geometric principles in various practical scenarios. Remember, always clarify the arrangement of points and angles for precise geometric calculations. The seemingly straightforward problem of finding AC reveals the depth and complexity of geometrical reasoning.
Latest Posts
Latest Posts
-
How To Find A1 In Arithmetic Sequence
May 09, 2025
-
Subtracting A Positive Integer From A Negative Integer
May 09, 2025
-
The Diagonals Of A Parallelogram Are Equal
May 09, 2025
-
Angle Pairs Worksheet Geometry Answer Key
May 09, 2025
-
What Is The Perimeter Of A Regular Pentagon
May 09, 2025
Related Post
Thank you for visiting our website which covers about Find Ac If Ab 16 And Bc 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.