Find The Area Of Irregular Figures Worksheet
News Co
Apr 07, 2025 · 7 min read
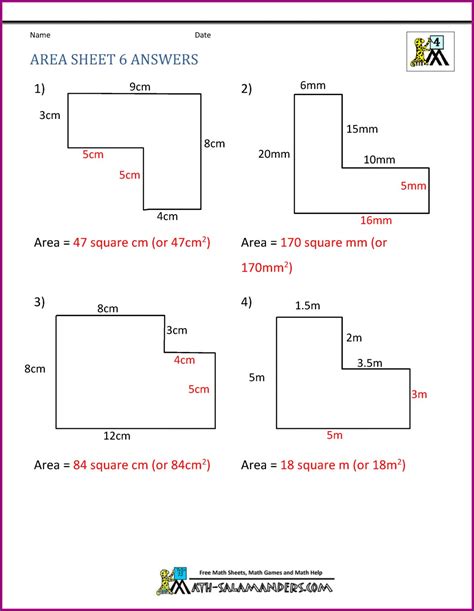
Table of Contents
Finding the Area of Irregular Figures: A Comprehensive Worksheet Guide
Calculating the area of regular shapes like squares, rectangles, and circles is straightforward. However, when faced with irregular figures, finding the area becomes a more challenging, yet crucial, skill in various fields, from architecture and engineering to surveying and graphic design. This comprehensive guide provides a step-by-step approach to tackling area calculations for irregular shapes, along with practical examples and helpful tips to master this essential skill. We'll explore various methods, from simple estimations to more complex mathematical techniques. Prepare to conquer your irregular area challenges!
Understanding Irregular Figures
Before diving into calculation methods, it's crucial to understand what constitutes an irregular figure. Simply put, an irregular figure is any shape that does not have the easily defined characteristics of a standard geometric shape. These shapes lack consistent, predictable angles and sides. Examples include:
- Amoebic shapes: These are shapes with uneven, blob-like outlines.
- Freeform shapes: These are shapes created without any specific geometric constraints.
- Complex polygons: These are polygons with an unequal number of sides and angles.
- Shapes with curved edges: These shapes incorporate curves as part of their boundaries.
The irregularity of these shapes makes applying standard area formulas (like those for rectangles or triangles) impossible. We need alternative approaches.
Methods for Calculating the Area of Irregular Figures
Several methods exist to determine the area of irregular shapes, each with its own level of accuracy and complexity. Let's explore some of the most common approaches:
1. Decomposition Method: Breaking Down Complex Shapes
The decomposition method involves dividing the irregular figure into several smaller, regular shapes (like rectangles, triangles, squares, or circles). This approach allows us to apply known area formulas to each individual component and then sum the results to find the total area.
Steps:
- Visualize the Divisions: Carefully examine the irregular figure and identify how to divide it into manageable regular shapes. This may involve drawing lines to create rectangles, triangles, or other recognizable shapes within the irregular shape.
- Calculate Individual Areas: Using the appropriate formula, calculate the area of each smaller regular shape.
- Sum the Areas: Add the areas of all the individual shapes to find the total area of the original irregular figure.
Example: Imagine an irregular figure that resembles a house. It can be decomposed into a rectangle (the main body) and a triangle (the roof). Calculate the areas separately, and then add them to get the total area of the house-shaped figure.
Advantages: Relatively simple and easy to understand, especially for shapes that can be easily divided. Disadvantages: Accuracy depends on the precision of the decomposition. Approximations may be necessary, leading to potential errors, particularly with highly irregular figures.
2. Grid Method: Counting Squares
The grid method provides a visual and relatively straightforward approach, particularly useful for estimating the area of figures with complex shapes. It involves overlaying a grid of equal-sized squares over the irregular figure.
Steps:
- Overlay a Grid: Draw a grid of squares (e.g., 1cm x 1cm) over the irregular figure.
- Count Full Squares: Count the number of squares that are completely enclosed within the figure.
- Estimate Partial Squares: Estimate the area of partially enclosed squares. You can approximate by considering the proportion of the square that falls within the figure (e.g., a half-square contributes 0.5 square units).
- Sum the Areas: Add the number of full squares and the estimated areas of the partial squares to obtain an approximate total area.
Advantages: Intuitive and easy to understand, especially for visual learners. Good for quick estimations. Disadvantages: The accuracy depends on the grid's size; finer grids provide greater accuracy but increase the counting effort. Estimating partial squares introduces a degree of error.
3. Using Geometry Software: Precise Calculations
Geometry software provides precise calculations of irregular areas. These software packages use advanced algorithms to calculate areas more accurately than manual methods. Examples include GeoGebra, AutoCAD, and various other CAD software packages.
Advantages: Offers superior precision, eliminating much of the estimation involved in manual methods. Faster and more efficient for complex shapes. Disadvantages: Requires access to and proficiency in using geometry software.
4. The Trapezoidal Rule (for curved boundaries): Approximating with Trapezoids
If the irregular figure has a curved boundary, the trapezoidal rule provides a numerical method for approximating the area. This method approximates the curve using a series of trapezoids.
Steps:
- Divide into Trapezoids: Divide the area under the curve into a number of equally spaced vertical strips. Each strip forms a trapezoid.
- Calculate Trapezoid Areas: Use the formula for the area of a trapezoid: Area = 0.5 * (b1 + b2) * h, where b1 and b2 are the lengths of the parallel sides (the heights of the strips at their respective ends), and h is the width of the strip.
- Sum the Areas: Add the areas of all the trapezoids to obtain an approximation of the total area under the curve. The more trapezoids used, the more accurate the approximation.
Advantages: Provides a more accurate approximation for curved boundaries than simple grid methods. Disadvantages: Requires understanding and applying the trapezoidal rule formula. Accuracy increases with the number of trapezoids, increasing calculation effort.
5. Coordinate Geometry: Using the Shoelace Theorem (for polygons)
The shoelace theorem, also known as Gauss's area formula, provides a method for calculating the area of a polygon given the coordinates of its vertices.
Steps:
-
Obtain Coordinates: List the (x, y) coordinates of the polygon's vertices in order (clockwise or counterclockwise).
-
Apply the Formula: The area is calculated using the following formula: Area = 0.5 * |(x1y2 + x2y3 + ... + xny1) - (y1x2 + y2x3 + ... + ynx1)|
Where:
- (xᵢ, yᵢ) are the coordinates of the i-th vertex.
- n is the number of vertices.
Advantages: Provides an exact area for polygons without needing to decompose the shape. Suitable for polygons with many sides. Disadvantages: Requires accurate coordinates for each vertex. The formula can be complex for polygons with a large number of vertices.
Practical Application: Worksheet Exercises
Let's solidify our understanding with some practical worksheet exercises. Remember to show your work step-by-step for better comprehension and to identify potential errors.
Exercise 1: Decomposition Method
An irregular figure is composed of a rectangle with dimensions 5 cm by 3 cm and a triangle with a base of 4 cm and a height of 2 cm. Find the total area of the irregular figure.
Exercise 2: Grid Method
An irregular figure is drawn on a 1 cm grid. It completely encloses 12 squares. It partially encloses 8 squares, each about half-covered. Estimate the area of the irregular figure.
Exercise 3: Trapezoidal Rule (Simplified)
An irregular figure is bounded by a curve. The area is approximated using two trapezoids. The lengths of the parallel sides of the first trapezoid are 2 cm and 4 cm, with a width of 3 cm. The lengths of the parallel sides of the second trapezoid are 4 cm and 6 cm, with a width of 3 cm. Calculate the approximate area.
Exercise 4: Shoelace Theorem
A polygon has the following vertices: (1, 1), (4, 1), (5, 3), (3, 4), (1, 3). Find the area of the polygon using the shoelace theorem.
Tips for Success
- Drawings: Always draw a clear diagram of the irregular figure. This will greatly aid in visualizing the decomposition or grid method.
- Units: Pay close attention to units (e.g., cm², m², in²). Ensure consistency throughout your calculations.
- Accuracy: Strive for accuracy in measurements and calculations. Avoid rounding off intermediate results too early, as this can accumulate errors.
- Check your work: After completing a calculation, review your steps to catch any mistakes.
- Practice: The more you practice, the more comfortable and proficient you’ll become in finding the area of irregular figures.
Conclusion
Calculating the area of irregular figures may initially seem daunting, but with a systematic approach and practice, you can master various methods and confidently tackle even the most complex shapes. Remember to choose the most appropriate method based on the shape's characteristics and the required level of accuracy. By understanding the principles outlined in this guide and working through the provided exercises, you'll develop the necessary skills to confidently handle area calculations of irregular figures in any context. Embrace the challenge, and you’ll find this skill incredibly rewarding and applicable in many areas.
Latest Posts
Latest Posts
-
Lowest Common Multiple Of 11 And 12
Apr 10, 2025
-
Is 70 An Even Or Odd Number
Apr 10, 2025
-
How Many Liters Are In 1000 Milliliters
Apr 10, 2025
-
What Are The Prime Factors Of 65
Apr 10, 2025
-
Which Of The Following Is The Strongest Correlation
Apr 10, 2025
Related Post
Thank you for visiting our website which covers about Find The Area Of Irregular Figures Worksheet . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.