Find The Height Of A Cone
News Co
Apr 05, 2025 · 5 min read
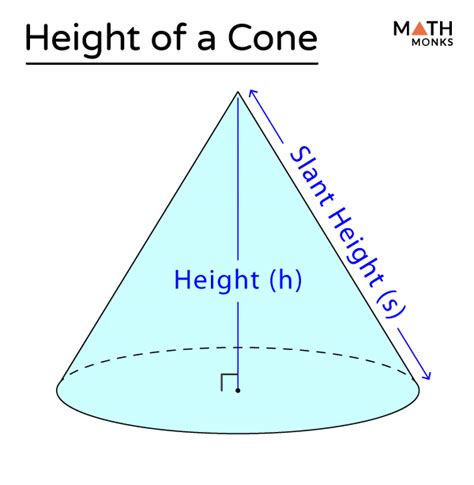
Table of Contents
Finding the Height of a Cone: A Comprehensive Guide
Determining the height of a cone is a fundamental problem in geometry with applications spanning various fields, from engineering and architecture to manufacturing and even culinary arts (think of perfectly shaped ice cream cones!). While the formula itself might seem straightforward, understanding the different scenarios and employing the correct method can be crucial for accurate results. This comprehensive guide will equip you with the knowledge and techniques to confidently calculate the height of a cone, regardless of the information provided.
Understanding the Cone and its Components
Before diving into the calculations, let's establish a clear understanding of the cone's key components:
- Height (h): The perpendicular distance from the apex (the pointy top) to the base. This is what we're aiming to find.
- Radius (r): The distance from the center of the circular base to any point on the circumference.
- Slant Height (l): The distance from the apex to any point on the circumference of the base. It's the hypotenuse of a right-angled triangle formed by the height, radius, and slant height.
- Base Area (A): The area of the circular base, calculated as πr².
- Volume (V): The amount of space enclosed by the cone, calculated as (1/3)πr²h.
Methods to Find the Height of a Cone
The method for finding the height of a cone depends on the information given. Here are the most common scenarios:
1. Using Radius and Volume
This is a common scenario, particularly in problems involving the capacity or volume of a cone-shaped container. If you know the volume (V) and the radius (r), you can rearrange the volume formula to solve for the height (h):
Formula: V = (1/3)πr²h
Solving for h: h = 3V / (πr²)
Example: A cone-shaped vase has a volume of 500 cubic centimeters and a radius of 10 centimeters. What is its height?
h = 3 * 500 cm³ / (π * (10 cm)²) ≈ 4.77 cm
2. Using Radius and Slant Height
When the slant height (l) and radius (r) are known, we can use the Pythagorean theorem, which applies to the right-angled triangle formed by the height, radius, and slant height:
Formula (Pythagorean Theorem): l² = r² + h²
Solving for h: h = √(l² - r²)
Example: A cone has a radius of 6 inches and a slant height of 10 inches. What is its height?
h = √(10² - 6²) = √(100 - 36) = √64 = 8 inches
3. Using Radius and Base Area
While less common, if the base area (A) and radius (r) are given, you can first find the radius and then use the radius and volume to calculate the height.
Formula (Base Area): A = πr²
Solving for r: r = √(A/π)
Once you have the radius, you can use method 1 (using radius and volume) or method 2 (using radius and slant height), provided the appropriate additional information is given.
4. Using Similar Cones
If you have a similar cone (a cone with the same shape but different size), you can use the ratios of corresponding sides to find the height. Let's say you have a larger cone with height H and radius R, and a smaller cone with height h and radius r. The ratio of corresponding sides will be the same:
Formula (Similar Cones): h/r = H/R
Solving for h: h = (r/R) * H
Example: A large cone has a height of 15 cm and a radius of 5 cm. A smaller cone, similar to the larger one, has a radius of 3 cm. What is the height of the smaller cone?
h = (3 cm / 5 cm) * 15 cm = 9 cm
Advanced Scenarios and Considerations
The scenarios discussed above cover the most common situations. However, some problems might require a more nuanced approach:
1. Frustums of Cones
A frustum is the portion of a cone that remains after its top has been cut off by a plane parallel to the base. Finding the height of a frustum requires additional information, such as the radii of the top and bottom bases, and possibly the slant height. This often involves more complex geometric calculations.
2. Cones within Cones
Problems might involve nested cones, where one cone sits inside another. Finding the height of one cone might require using the dimensions of the other cone.
3. Real-World Applications and Approximations
In real-world situations, measurements might not be perfectly precise. You might need to account for measurement error when calculating the height. For example, measuring the diameter of a cone's base would need to be accounted for using the radius (radius = diameter/2)
4. Using Calculus for Irregular Cones
For cones with irregular bases or curved sides, more advanced mathematical techniques such as calculus might be necessary to accurately calculate the height.
Practical Tips and Troubleshooting
- Units: Always ensure that all your measurements are in the same units. Converting units is a common source of error.
- Rounding: Be mindful of rounding errors. Avoid rounding intermediate calculations; round only your final answer to the appropriate number of significant figures.
- Draw a Diagram: Sketching a diagram of the cone and labeling its dimensions can greatly assist in visualizing the problem and choosing the correct approach.
- Check Your Work: Once you have calculated the height, check your answer using an alternative method or by verifying your work with a different calculation.
Conclusion
Finding the height of a cone is a fundamental geometrical problem that appears in various applications. By understanding the different methods, considering possible scenarios, and adhering to good mathematical practices, you can confidently tackle this problem and accurately determine the height of any cone, irrespective of the given parameters. Remember to always check your work and consider potential real-world implications affecting the accuracy of measurements. This comprehensive guide serves as a reliable resource for addressing any height-of-a-cone related query, from simple to advanced calculations. Mastering this skill not only enhances your mathematical prowess but also equips you to solve practical problems across various fields, demonstrating a clear understanding of geometrical principles.
Latest Posts
Latest Posts
-
What Percent Of 75 Is 90
Apr 05, 2025
-
What Is A Three Out Of Five
Apr 05, 2025
-
What Is The Square Root Of 170
Apr 05, 2025
-
Fraction Word Problems For 4th Graders
Apr 05, 2025
-
How Do You Spell The Number 30
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Find The Height Of A Cone . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
