Find The Lcm Of 12 And 15
News Co
Mar 21, 2025 · 5 min read
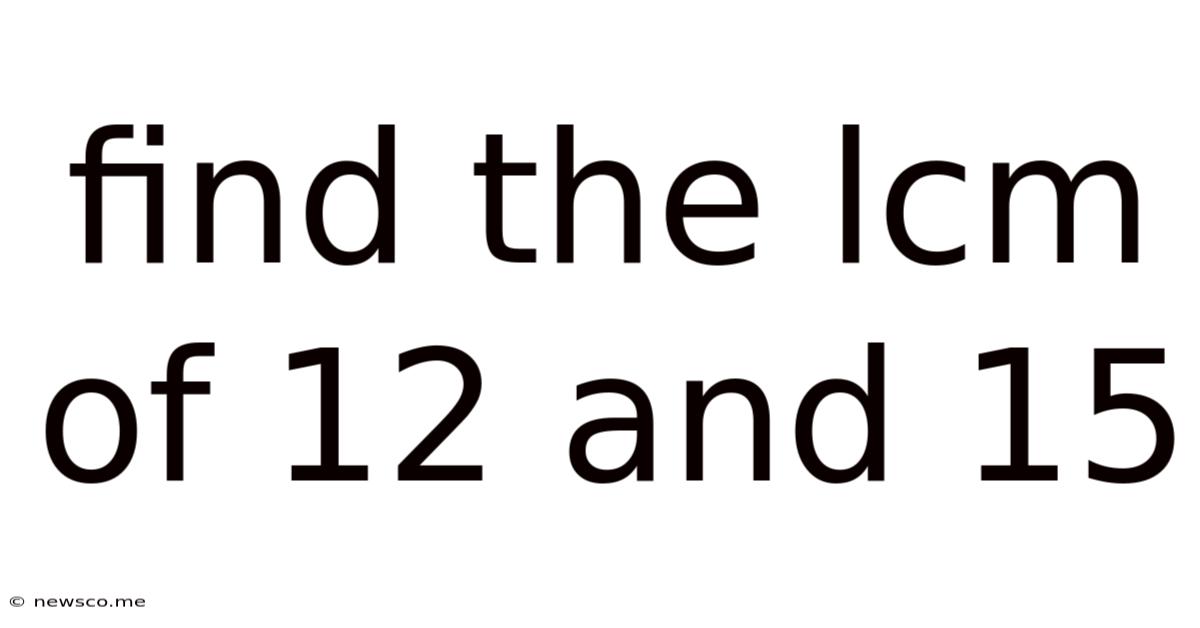
Table of Contents
Finding the LCM of 12 and 15: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly useful in various fields like simplifying fractions, solving problems involving cycles, and understanding rhythmic patterns. This comprehensive guide will delve into the process of finding the LCM of 12 and 15, exploring multiple methods and providing a detailed explanation of the underlying principles. We'll also touch upon the broader applications of LCMs in various contexts.
Understanding Least Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 12 and 15, let's solidify our understanding of the LCM concept. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that all the numbers you're considering can divide into evenly.
For instance, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18... Multiples of 3 are 3, 6, 9, 12, 15, 18... The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple (LCM) is the smallest of these common multiples, which is 6.
Method 1: Listing Multiples
The most straightforward method to find the LCM is by listing the multiples of each number until a common multiple is found. Let's apply this to 12 and 15:
Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120...
Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120...
Notice that 60 appears in both lists. However, a smaller common multiple, 60, is found first. Therefore, the LCM of 12 and 15 is 60.
This method works well for smaller numbers but can become cumbersome with larger numbers.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, involves prime factorization. This method breaks down each number into its prime factors—numbers that are only divisible by 1 and themselves. Then, we construct the LCM using the highest powers of all the prime factors present in the numbers.
Let's factorize 12 and 15:
- 12 = 2² × 3 (2 multiplied by itself twice, then multiplied by 3)
- 15 = 3 × 5
Now, to find the LCM, we take the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Multiply these together: 2² × 3 × 5 = 4 × 3 × 5 = 60
Therefore, the LCM of 12 and 15 using prime factorization is 60. This method is generally preferred for its efficiency and applicability to larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of two numbers are related through a simple formula:
LCM(a, b) × GCD(a, b) = a × b
Where 'a' and 'b' are the two numbers.
First, let's find the GCD of 12 and 15 using the Euclidean algorithm:
- Divide the larger number (15) by the smaller number (12): 15 ÷ 12 = 1 with a remainder of 3.
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (3): 12 ÷ 3 = 4 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 3.
So, GCD(12, 15) = 3.
Now, using the formula:
LCM(12, 15) = (12 × 15) / GCD(12, 15) = (180) / 3 = 60
This method provides an alternative approach to finding the LCM, particularly useful when the GCD is easily determined.
Applications of LCM
The concept of LCM extends beyond simple mathematical exercises; it finds practical applications in diverse fields:
1. Fraction Addition and Subtraction:
Finding a common denominator when adding or subtracting fractions requires determining the LCM of the denominators. For example, to add 1/12 and 1/15, we need to find the LCM of 12 and 15 (which is 60), and then express both fractions with a denominator of 60 before adding them.
2. Cyclic Events:
LCM helps determine when cyclical events will coincide. Imagine two traffic lights, one changing every 12 seconds and the other every 15 seconds. The LCM (60 seconds) tells us when both lights will simultaneously be green (assuming a simple cycle).
3. Scheduling and Planning:
In project management or scheduling, determining when different tasks or processes will align often involves calculating LCMs. For example, two machines operating at different cycles may need their maintenance schedules coordinated using LCM calculations.
4. Music and Rhythm:
Musical rhythms and patterns often rely on LCM. Finding the LCM of different note durations helps determine when different rhythmic patterns will coincide, leading to harmonious or complex musical structures.
Conclusion: Finding the LCM of 12 and 15
Through various methods – listing multiples, prime factorization, and using the GCD – we've conclusively demonstrated that the least common multiple of 12 and 15 is 60. Understanding these different approaches allows you to choose the most efficient method depending on the numbers involved. More importantly, grasping the concept of LCM opens doors to solving a wide range of problems across various disciplines, showcasing its significance in both theoretical mathematics and practical applications. Remember, the key is to choose the method that best suits your needs and comfort level. Practice with different numbers to solidify your understanding and mastery of this important mathematical concept. The versatility and practical applications of LCM make it a crucial tool for anyone working with numbers, whether in mathematics, science, engineering, or even music.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Find The Lcm Of 12 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.