Find The Lcm Of 12 And 8
News Co
Mar 17, 2025 · 5 min read
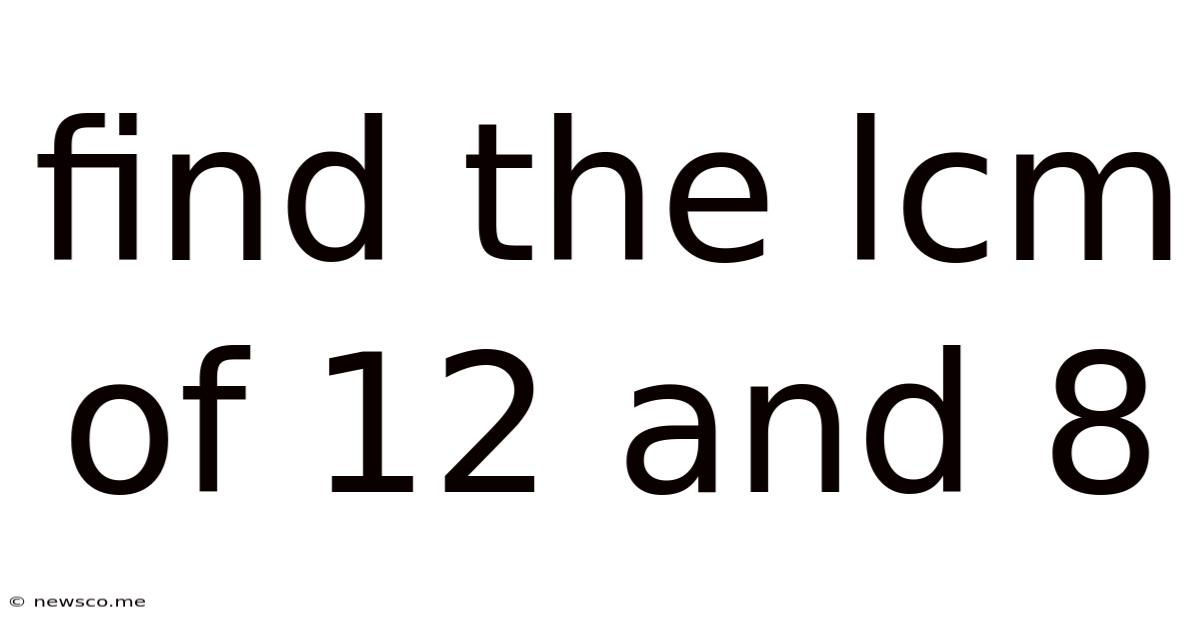
Table of Contents
Finding the Least Common Multiple (LCM) of 12 and 8: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics with applications spanning various fields, from scheduling tasks to simplifying fractions. This comprehensive guide will explore different methods to find the LCM of 12 and 8, providing a thorough understanding of the process and its underlying principles. We'll delve into the concept of LCM, explain why it's important, and demonstrate multiple techniques to calculate it effectively. Furthermore, we’ll explore the relationship between LCM and the greatest common divisor (GCD), and apply the LCM to real-world problems.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
Why is LCM important?
The concept of LCM has significant applications in various areas:
- Fraction Operations: Finding a common denominator when adding or subtracting fractions requires determining the LCM of the denominators.
- Scheduling Problems: Determining when events will occur simultaneously often involves finding the LCM of their periods. For example, two machines running at different cycles will coincide at a time interval equal to the LCM of their individual cycles.
- Modular Arithmetic: LCM plays a critical role in solving problems related to modular arithmetic, which has applications in cryptography and computer science.
- Music Theory: LCM is used in understanding musical intervals and harmonies.
Methods for Finding the LCM of 12 and 8
Let's now explore different methods to calculate the LCM of 12 and 8:
1. Listing Multiples Method
This is a straightforward method, especially suitable for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120...
Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120...
By comparing the lists, we find that the smallest common multiple is 24. Therefore, the LCM(12, 8) = 24.
This method is simple but can become cumbersome with larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
Prime factorization of 12: 2² x 3
Prime factorization of 8: 2³
To find the LCM, we take the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
Therefore, LCM(12, 8) = 2³ x 3 = 8 x 3 = 24.
This method is generally more efficient than listing multiples, especially when dealing with larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD of two numbers are related by the following formula:
LCM(a, b) x GCD(a, b) = a x b
First, we need to find the GCD of 12 and 8. We can use the Euclidean algorithm for this:
- Divide the larger number (12) by the smaller number (8): 12 = 1 x 8 + 4
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (4): 8 = 2 x 4 + 0
The last non-zero remainder is the GCD, which is 4.
Now, we can use the formula:
LCM(12, 8) = (12 x 8) / GCD(12, 8) = (12 x 8) / 4 = 24
This method is efficient and provides a connection between LCM and GCD.
4. Ladder Method (Prime Factorization using a ladder diagram)
This visual method simplifies the prime factorization process.
12 | 2
6 | 2
3 | 3
1 |
8 | 2
4 | 2
2 | 2
1 |
We list the prime factors of 12 and 8 side-by-side, performing prime factorization for each number. Then, we multiply the highest power of each prime factor to obtain the LCM. In this case, the highest powers are 2³ and 3¹, resulting in LCM = 2³ * 3 = 24.
Real-World Applications of LCM
Let's illustrate the practical applications of LCM with some examples:
Example 1: Scheduling Tasks
Imagine you have two machines. Machine A completes a cycle every 12 minutes, and Machine B completes a cycle every 8 minutes. When will both machines complete a cycle simultaneously?
The answer is the LCM(12, 8) = 24 minutes. Both machines will complete a cycle together every 24 minutes.
Example 2: Fraction Addition
To add the fractions 1/12 and 1/8, we need to find a common denominator. The LCM of 12 and 8 is 24.
1/12 + 1/8 = (2/24) + (3/24) = 5/24
Example 3: Musical Rhythms
Suppose a musical piece has a rhythm pattern repeating every 12 beats, and another rhythm pattern repeating every 8 beats. The LCM will determine when both rhythm patterns coincide perfectly. The LCM(12, 8) = 24 beats, so they align perfectly every 24 beats.
Conclusion: Mastering the LCM
Finding the least common multiple is a crucial skill with widespread applications. This guide has explored multiple methods – listing multiples, prime factorization, using the GCD, and the ladder method – allowing you to choose the most efficient approach depending on the numbers involved. Understanding these methods and their application to real-world problems will significantly enhance your mathematical problem-solving abilities. Remember that the choice of method often depends on the size and complexity of the numbers. For smaller numbers, the listing method might suffice, while prime factorization or the GCD method becomes more efficient for larger numbers. The ladder method provides a visually appealing alternative to prime factorization. No matter the method, the core concept remains the same: finding the smallest positive integer that is a multiple of all the given numbers.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Find The Lcm Of 12 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.